
����Ŀ����ͼ������ߣ������ɷ����ǣ�I�����������Σ�ͼ��1������ÿ�����ȷ֣������м����һ���߶�Ϊһ�ױ����������ȱ������Σ�Ȼ��ȥ���ױߣ��õ�ͼ��2����(II)��ͼ��2����ÿ�����ȷ֣��ظ���������ͼ�������õ�ͼ��3����(III)�ٰ�����������������ȥ�����õ������߳�Ϊѩ������(Koch��Snowflake)��
![]()
 ��1��
��1�� ��2��
��2��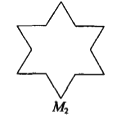 ��3��
��3��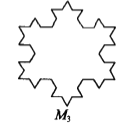 .
.
��ͼ��1���ĵȱ������εı߳�Ϊ1�����ҷֱ�ͼ��1������2������3�����е�ͼ�����μ���M1��M2��M3����![]() ��
��
��1����![]() �еı���Ϊ
�еı���Ϊ![]() ��ÿ���ߵij���Ϊ
��ÿ���ߵij���Ϊ![]() ��д������
�������![]() ��
��![]() �ĵ��ƹ�ʽ��ͨ�ʽ��
�ĵ��ƹ�ʽ��ͨ�ʽ��
��2����![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ��
��![]() ��Χ�ɵ����Ϊ
��Χ�ɵ����Ϊ![]() ��������{
��������{![]() }��{
}��{![]() }��ͨ�ʽ�������ܳ�
}��ͨ�ʽ�������ܳ�![]() �����
�����![]() �ļ����Ƿ���ڣ������ڣ�����ü��ޣ��������ڣ���˵������.
�ļ����Ƿ���ڣ������ڣ�����ü��ޣ��������ڣ���˵������.
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �� ��2��
�� ��2��![]() ��
��![]() ���ܳ�
���ܳ�![]() �ļ������ڣ����
�ļ������ڣ����![]() �ļ���Ϊ
�ļ���Ϊ![]() .
.
��������
��1���������⣬���ͼ�εı任���ֱ�ó�����![]() ��
��![]() �ĵ��ƹ�ϵʽ����ϵȱ����е�ͨ�ʽ��������⣻
�ĵ��ƹ�ϵʽ����ϵȱ����е�ͨ�ʽ��������⣻
��2������ͼ��ı任���ɣ��ó�����![]() ��
��![]() �ĵ��ƹ�ϵʽ����ϵ��ӷ������еļ��ޣ��������.
�ĵ��ƹ�ϵʽ����ϵ��ӷ������еļ��ޣ��������.
��1�������⣬�ɵ�����![]() �ĵ��ƹ�ϵʽΪ
�ĵ��ƹ�ϵʽΪ![]() ��
��![]() ��
��
��������![]() ��������Ϊ
��������Ϊ![]() ������Ϊ4�ĵȱ����У�
������Ϊ4�ĵȱ����У�
������ͨ�ʽΪ![]() ��
��
����ÿ��ͼ�εı߳�����ȣ��ҳ��ȱ�Ϊԭ����![]() ��
��
���Ա߳�![]() ������ƹ�ϵʽ
������ƹ�ϵʽ![]() ��
��
������![]() ��������Ϊ1������Ϊ
��������Ϊ1������Ϊ![]() �ĵȱ����У�
�ĵȱ����У�
��������![]() ��ͼͨ�ʽΪ
��ͼͨ�ʽΪ![]()
��2���۲췢�֣��ڶ���ͼ���ڵ�һ��ͼ�ε��ܳ��Ļ����϶��������ܳ���![]() ��������ͼ���ڵڶ������ܳ��Ļ����ϣ������ܳ���
��������ͼ���ڵڶ������ܳ��Ļ����ϣ������ܳ���![]() �����ĸ�ͼ���ڵ��������ܳ��Ļ����ϣ������ܳ���
�����ĸ�ͼ���ڵ��������ܳ��Ļ����ϣ������ܳ���![]() ���������ƣ�
���������ƣ�
�ɵ��ܳ�![]() ������ƹ�ϵʽ
������ƹ�ϵʽ![]() ��
��![]() ��
��
��������![]() ��������Ϊ3������Ϊ
��������Ϊ3������Ϊ![]() �ĵȱ����У�
�ĵȱ����У�
��������![]() ��ͨ�ʽΪ
��ͨ�ʽΪ![]() ��
��
�ɵ�һ�������ε����![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]()
 .
.
���ɼ������㷨�ɵ�![]() �������ܳ�
�������ܳ�![]() �ļ������ڣ�
�ļ������ڣ�
![]() �������
�������![]() �ļ���Ϊ
�ļ���Ϊ![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1��������![]() �뺯��
�뺯��![]() �ڵ�
�ڵ�![]() ���й�ͬ������
���й�ͬ������![]() ����
����![]() ��ֵ��
��ֵ��
��2��֤����![]() ��
��
��3��������ʽ![]() ������
������![]() ��
��![]() ����������ʵ��
����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
�� ![]() ��ʾ������ͬ��ֱ�ߣ�
��ʾ������ͬ��ֱ�ߣ� ![]() ��
�� ![]() ��
�� ![]() ��ʾ������ͬ��ƽ�棬���������ĸ����⣺
��ʾ������ͬ��ƽ�棬���������ĸ����⣺
��![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
��
��![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
��
��![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
��
��![]() ��
�� ![]() ��
�� ![]() ����
����![]()
������ȷ��������Ϊ�� ��
A. �٢� B. �ڢ� C. �ۢ� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ![]() ��������Ϊ
��������Ϊ![]() ����Բ
����Բ![]() ��һ��
��һ��![]() ��������������
��������������![]() �ľ���֮����4.
�ľ���֮����4.
��1������Բ�ķ��̣�
��2����֪��![]() ��ֱ������Բ
��ֱ������Բ![]() ����
����![]() ���㣬�����������Ҷ��㲻�غϣ���
���㣬�����������Ҷ��㲻�غϣ���![]() �����ı���
�����ı���![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
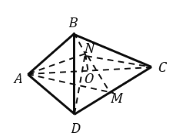
����Ŀ����֪������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() �ضԽ���
�ضԽ���![]() ����ʹƽ��
����ʹƽ��![]() ƽ��
ƽ��![]() ���õ���ͼ��ʾ������
���õ���ͼ��ʾ������![]() ����
����![]() Ϊ
Ϊ![]() �ߵ��е㣬
�ߵ��е㣬![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �ϵĶ��㣨�������˵㣩����
�ϵĶ��㣨�������˵㣩����![]() ����
����![]() ��������
��������![]() �����ȡ�����ֵʱ������
�����ȡ�����ֵʱ������![]() ��������İ뾶Ϊ_______.
��������İ뾶Ϊ_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=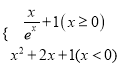 ��������y=f��f��x����a����1��������㣬��a��ȡֵ��Χ��_____��
��������y=f��f��x����a����1��������㣬��a��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������3x+3y+8��2xy��x��0��y��0��������x��y����x+y��2��a��x+y��+16��0���������ʵ��a��ȡֵ��Χ�ǣ�������
A.��������8]B.[8��+����C.��������10]D.[10��+����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ABECD��һ��ֱ������ABCD��һ���ȱ�������BCE���ɣ���ͼ1��ʾ,AB�ABC��AB//CD����AB=2CD��������ABCD����BC������ͼ2��ʾ����AB�Aƽ��BEC��
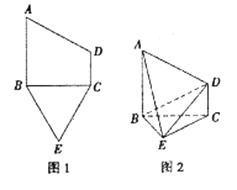
(1)��֤:ƽ��ABE�Aƽ��ADE��
(2)��AB=BC,������A-DE-B������ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com