
【题目】已知奇函数![]() 的导函数为
的导函数为![]() ,且
,且![]() ,当
,当![]() 时
时![]() 恒成立,则使得
恒成立,则使得![]() 成立的
成立的![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题意构造函数g(x)=xf(x),结合条件可得到函数g(x)的单调性和奇偶性,结合函数g(x)的单调性、奇偶性画出函数的大致图象,由图象可得x的取值范围.
由题意设g(x)=xf(x),则g′(x)=xf′(x)+f(x),
∴当x>0时,g′(x)>0,函数g(x)在(0,+∞)上为增函数,
∵函数f(x)是奇函数,
∴g(﹣x)=(﹣x)f(﹣x)=(﹣x)[﹣f(x)]=xf(x)=g(x),
∴函数g(x)为定义域上的偶函数,
由f(﹣1)=0得,g(﹣1)=0,函数g(x)的图象大致如图:
∵不等式f(x)>0![]() ,∴
,∴![]() 或
或![]() ,
,
由函数的图象得,﹣1<x<0或x>1,
∴使得f(x)>0成立的x的取值范围是:(﹣1,0)∪(1,+∞),
故选:C.



科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.已知幂函数![]() 在
在![]() 上单调递减则
上单调递减则![]() 或
或![]()
B.函数![]() 的有两个零点,一个大于0,一个小于0的一个充分不必要条件是
的有两个零点,一个大于0,一个小于0的一个充分不必要条件是![]() .
.
C.已知函数![]() ,若
,若![]() ,则
,则![]() 的取值范围为
的取值范围为![]()
D.已知函数![]() 满足
满足![]() ,
,![]() ,且
,且![]() 与
与![]() 的图像的交点为
的图像的交点为![]() 则
则![]() 的值为8
的值为8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
, ![]() ,外接球的球心为
,外接球的球心为![]() ,点
,点![]() 是侧棱
是侧棱![]() 上的一个动点.有下列判断:
上的一个动点.有下列判断:
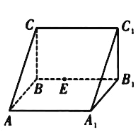
① 直线![]() 与直线
与直线![]() 是异面直线;②
是异面直线;②![]() 一定不垂直
一定不垂直![]() ;
;
③ 三棱锥![]() 的体积为定值; ④
的体积为定值; ④![]() 的最小值为
的最小值为![]() .
.
其中正确的序号序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各级城市的大街小巷,为了解我市的市民对共享单车的满意度,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了50人进行分析.若得分低于60分,说明不满意,若得分不低于60分,说明满意,调查满意度得分情况结果用茎叶图表示如图1.
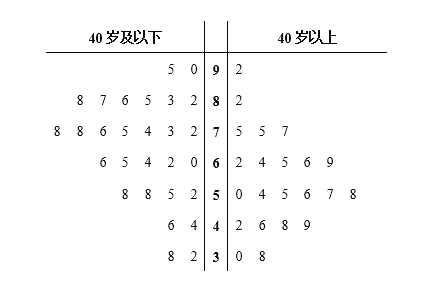
(Ⅰ)根据茎叶图找出40岁以上网友中满意度得分的众数和中位数;
(Ⅱ)根据茎叶图完成下面列联表,并根据以上数据,判断是否有![]() 的把握认为满意度与年龄有关;
的把握认为满意度与年龄有关;
满意 | 不满意 | 合计 | |
40岁以下 | |||
40岁以上 | |||
合计 |
(Ⅲ)先采用分层抽样的方法从40岁及以下的网友中选取7人,再从这7人中随机选出2人,将频率视为概率,求选出的2人中至少有1人是不满意的概率.
参考格式: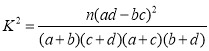 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
(Ⅰ)若点P在椭圆C的内部,求直线AM的斜率的取值范围;
(Ⅱ)设椭圆C的右焦点为F,点Q在y轴上,且∠PFQ=90°,求证:AQ∥BM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对给定的d∈N*,记由数列构成的集合![]() .
.
(1)若数列{an}∈Ω(2),写出a3的所有可能取值;
(2)对于集合Ω(d),若d≥2.求证:存在整数k,使得对Ω(d)中的任意数列{an},整数k不是数列{an}中的项;
(3)已知数列{an},{bn}∈Ω(d),记{an},{bn}的前n项和分别为An,Bn.若|an+1|≤|bn+1|,求证:An≤Bn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com