
【题目】已知△ABC中,角A,B,C所对的边分别为a,b,c,若(2b﹣c)cosA=acosC.
(1)求角A;
(2)若△ABC的外接圆面积为π,求△ABC的面积的最大值.
【答案】(1)A![]() (2)
(2)![]() .
.
【解析】
(1)化边为角,利用两角和正弦公式,即可求解;
(2)由正弦定理求出![]() ,
,![]() 和角
和角![]() 应用余弦定理建立
应用余弦定理建立![]() 关系,再由基本不等式求出
关系,再由基本不等式求出![]() 最大值,即可求出结论.
最大值,即可求出结论.
(1)∵(2b﹣c)cosA=acosC,
∴由正弦定理可得:(2sinB﹣sinC)cosA=sinAcosC,
可得:2sinBcosA=sinAcosC+sinCcosA=sinB,
∵sinB≠0,∴cosA![]() ,∵0<A<π,∴A
,∵0<A<π,∴A![]() ,
,
(2)∵△ABC的外接圆面积为π,
∴△ABC的外接圆半径为1,∵![]() ,∴a
,∴a![]() ,
,
∵由余弦定理可得a2=b2+c2﹣2bccosA,
可得3=b2+c2﹣bc≥2bc﹣bc=bc,
∴bc≤3,当且仅当b=c![]() 等号成立,
等号成立,
∴S△ABC![]() bcsinA
bcsinA![]() ,当且仅当b=c
,当且仅当b=c![]() 等号成立,
等号成立,
∴S△ABC的最大值为![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是由
是由![]() 个有序实数构成的一个数组,记作:
个有序实数构成的一个数组,记作:![]() .其中
.其中![]() 称为数组
称为数组![]() 的“元”,
的“元”,![]() 称为
称为![]() 的下标,如果数组
的下标,如果数组![]() 中的每个“元”都是来自数组
中的每个“元”都是来自数组![]() 中不同下标的“元”,则称
中不同下标的“元”,则称![]() 为
为![]() 的子数组.定义两个数组
的子数组.定义两个数组![]() ,
,![]() 的关系数为
的关系数为![]() .
.
(1)若![]() ,
,![]() ,设
,设![]() 是
是![]() 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求![]() 的最大值;
的最大值;
(2)若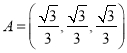 ,
,![]() ,且
,且![]() ,
,![]() 为
为![]() 的含有三个“元”的子数组,求
的含有三个“元”的子数组,求![]() 的最大值;
的最大值;
(3)若数组![]() 中的“元”满足
中的“元”满足![]() ,设数组
,设数组![]() 含有四个“元”
含有四个“元”![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的所有含有三个“元”的子数组的关系数
的所有含有三个“元”的子数组的关系数![]() (
(![]() )的最大值.
)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某投资公司在2010年年初准备将1000万元投资到“低碳”项目上,现有两个项目供选择:
项目一:新能源汽车.据市场调研,投资到该项目上,到年底可能获利![]() ,也可能亏损
,也可能亏损![]() ,且这两种情况发生的概率分别为
,且这两种情况发生的概率分别为![]() 和
和![]() ;
;
项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利![]() ,可能亏损
,可能亏损![]() ,也可能不赔不赚,且这三种情况发生的概率分别为
,也可能不赔不赚,且这三种情况发生的概率分别为![]() 、
、![]() 和
和![]()
(Ⅰ)针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由;
(Ⅱ)若市场预期不变,该投资公司按照你选择的项目长期投资(每一年的利润和本金继续用作投资),问大约在哪一年的年底总资产(利润+本金)可以翻一番?
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为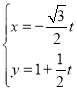 ,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2
,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2![]() sinθ,
sinθ,
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)直线l与x轴交于点P,与曲线C交于A,B两点,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
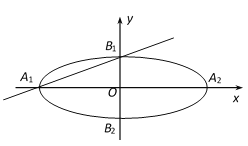
【题目】在平面直角坐标系![]() 中,如图,已知椭圆E:
中,如图,已知椭圆E:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() .设直线
.设直线![]() 倾斜角的余弦值为
倾斜角的余弦值为![]() ,圆
,圆![]() 与以线段
与以线段![]() 为直径的圆关于直线
为直径的圆关于直线![]() 对称.
对称.
(1)求椭圆E的离心率;
(2)判断直线![]() 与圆
与圆![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆![]() 的面积为
的面积为![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设θ∈[0,π],且f(θ)![]() 1,求θ的值;
1,求θ的值;
(2)在△ABC中,AB=1,f(C)![]() 1,且△ABC的面积为
1,且△ABC的面积为![]() ,求sinA+sinB的值.
,求sinA+sinB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x+3|+|2x﹣1|.
(1)求不等式f(x)≤6的解集;
(2)若关于x的不等式f(x)<|m﹣1|的解集非空,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com