
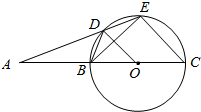
 已知圆O,点A为圆O外一点,BC为圆O的直径,过A作圆O的割线交圆O于D,E两点,其满足BD=DE.
已知圆O,点A为圆O外一点,BC为圆O的直径,过A作圆O的割线交圆O于D,E两点,其满足BD=DE.分析 (1)如图,连接DC,由圆周角定理和圆周角、弧、弦间的关系进行推理;
(2)欲求四边形BDEC的周长,只需得到圆的半径即可.根据(1)的结论得到OD∥EC,由平行线截线段成比例得到半径的长度.
解答  (1)证明:如图,连接DC.
(1)证明:如图,连接DC.
∵BD=DE,
∴∠BCD=∠ECD,即∠ECA=2∠BCD.
又∵∠DOB=2∠BCD,
∴∠DOB=∠ECA;
(2)解:由(1)知,∠DOB=∠ECA,则OD∥EC,
∵AB=BO,BD=DE=1,OB=OC=OD,
∴$\frac{AD}{AE}$=$\frac{AO}{AC}$=$\frac{OD}{EC}$,则$\frac{AD}{DE}$=$\frac{2OB}{OB}$.
∴$\frac{AD}{1}$=2,
则AD=2,AE=3,EC=$\frac{3}{2}$OD,
又AD•AE=AB•AC,即2×3=OB•3OB,
∴OB=$\sqrt{2}$,
∴四边形BDEC的周长是:BD+DE+EC+BC=2+$\frac{3}{2}$OD+OB=2+$\frac{5\sqrt{2}}{2}$.
点评 本题考查了圆周角定理和相交弦定理.一条弧所对的圆周角等于它所对的圆心角的一半.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:填空题
 两个半径分别为r1,r2的圆M,N,公共弦AB长为3,如图所示,则$\overrightarrow{AM}•\overrightarrow{AB}+\overrightarrow{AN}•\overrightarrow{AB}$=9.
两个半径分别为r1,r2的圆M,N,公共弦AB长为3,如图所示,则$\overrightarrow{AM}•\overrightarrow{AB}+\overrightarrow{AN}•\overrightarrow{AB}$=9.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{5}{6}$ | C. | 2 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证:
如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
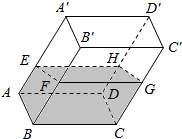 如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.
如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com