
【题目】已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,则( )
对称,则( )
A.函数![]() 为奇函数
为奇函数
B.函数![]() 在
在![]() 上单调递增
上单调递增
C.若![]() ,则
,则![]() 的最小值为
的最小值为![]()
D.函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象
的图象
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】根据《环境空气质量指数![]() 技术规定(试行)》规定:空气质量指数在区间
技术规定(试行)》规定:空气质量指数在区间![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时,其对应的空气质量状况分别为优、良、轻度污染、中度污染、重度污染、严重污染.如图为某市2019年10月1日至10月7日的空气质量指数
时,其对应的空气质量状况分别为优、良、轻度污染、中度污染、重度污染、严重污染.如图为某市2019年10月1日至10月7日的空气质量指数![]() 直方图,在这7天内,下列结论正确的是( )
直方图,在这7天内,下列结论正确的是( )
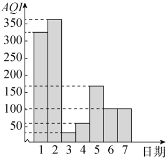
A.前4天![]() 的方差小于后3天
的方差小于后3天![]() 的方差
的方差
B.这7天内空气质量状况为严重污染的天数为3
C.这7天的平均空气质量状况为良
D.空气质量状况为优或良的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个调查学生记忆力的研究团队从某中学随机挑选100名学生进行记忆测试,通过讲解100个陌生单词后,相隔十分钟进行听写测试,间隔时间![]() (分钟)和答对人数
(分钟)和答对人数![]() 的统计表格如下:
的统计表格如下:
时间 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
答对人数 | 98 | 70 | 52 | 36 | 30 | 20 | 15 | 11 | 5 | 5 |
| 1.99 | 1.85 | 1.72 | 1.56 | 1.48 | 1.30 | 1.18 | 1.04 | 0.7 | 0.7 |
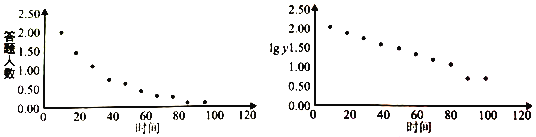
时间![]() 与答对人数
与答对人数![]() 的散点图如图:
的散点图如图:
附:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对于一组数据
,对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: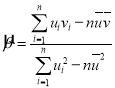 ,
,![]() .请根据表格数据回答下列问题:
.请根据表格数据回答下列问题:
(1)根据散点图判断,![]() 与
与![]() ,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
,哪个更适宣作为线性回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果,建立![]() 与
与![]() 的回归方程;(数据保留3位有效数字)
的回归方程;(数据保留3位有效数字)
(3)根据(2)请估算要想记住![]() 的内容,至多间隔多少分钟重新记忆一遍.(参考数据:
的内容,至多间隔多少分钟重新记忆一遍.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)问:![]() 的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4-4:坐标系与参数方程)
在直角坐标系![]() 中,半圆C的参数方程为
中,半圆C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以O为极点,x轴的非负半轴为极轴建立极坐标系.
),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求C的极坐标方程;
(Ⅱ)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线OM:
,射线OM:![]() 与半圆C的交点为O、P,与直线
与半圆C的交点为O、P,与直线![]() 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的检验员为了检测生产线上生产零件的情况,从产品中随机抽取了![]() 个进行测量,根据所测量的数据画出频率分布直方图如下:
个进行测量,根据所测量的数据画出频率分布直方图如下:

如果:尺寸数据在![]() 内的零件为合格品,频率作为概率.
内的零件为合格品,频率作为概率.
(1)从产品中随机抽取![]() 件,合格品的个数为
件,合格品的个数为![]() ,求
,求![]() 的分布列与期望:
的分布列与期望:
(2)为了提高产品合格率,现提出![]() ,
,![]() 两种不同的改进方案进行试验,若按
两种不同的改进方案进行试验,若按![]() 方案进行试验后,随机抽取
方案进行试验后,随机抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() :若按
:若按![]() 方案试验后,抽取
方案试验后,抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ,你会选择哪个改进方案?
,你会选择哪个改进方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com