
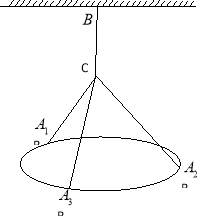
【题目】一吊灯下沿圆环直径为![]() 米,通过拉链
米,通过拉链![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() 、
、![]() 、
、![]() 是圆上三等份点)悬挂在
是圆上三等份点)悬挂在![]() 处,圆环呈水平状态并距天花板2米,如图所示.
处,圆环呈水平状态并距天花板2米,如图所示.
(1)为使拉链总长最短,![]() 应多长?
应多长?
(2)为美观与安全,在圆环上设置![]() ,
,![]() ,……,
,……,![]() (
(![]() )各等分点,仍按上面方法连接.若还要求拉链总长度最短,对比(1)时C点位置,此时C点将会上移还是会下移?请说明理由.
)各等分点,仍按上面方法连接.若还要求拉链总长度最短,对比(1)时C点位置,此时C点将会上移还是会下移?请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 点的位置将下移.
点的位置将下移.
【解析】
试题分析:(1)设![]() 离天花板
离天花板![]() 米(
米(![]() ),拉链总长度为
),拉链总长度为![]() 米,利用所给图,得到
米,利用所给图,得到![]() ,其导,利用导数求出
,其导,利用导数求出![]() 取何值时,
取何值时,![]() 最小;(2)当在圆环上设置
最小;(2)当在圆环上设置![]() 个点时,拉链的总长为
个点时,拉链的总长为![]() ,同样利用导数求出
,同样利用导数求出![]() 取何值时,
取何值时,![]() 最小.并与(1)中值比较,可知
最小.并与(1)中值比较,可知![]() 点的位置移动情况.
点的位置移动情况.
试题解析:
(1)设![]() 离天花板
离天花板![]() 米(
米(![]() ),拉链总长度为
),拉链总长度为![]() 米,由题意
米,由题意![]() 、
、![]() 、
、![]() 、
、![]() 四点构成一个正三棱锥,
四点构成一个正三棱锥,![]() 、
、![]() 、
、![]() 为该三棱锥的三条棱侧,三棱锥的高
为该三棱锥的三条棱侧,三棱锥的高
![]() .于是有
.于是有![]() ,对其求导,得
,对其求导,得![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,![]() 时,即
时,即![]() 米时,
米时,![]() 取最小值
取最小值![]() 米.
米.
(2)由(1)可知,当在圆环上设置![]() 个点时,拉链的总长为:
个点时,拉链的总长为:![]() ,求导得
,求导得![]() ,当
,当![]() 时,
时,![]() .解之得
.解之得![]() ,因为
,因为![]() 只有一个极值,所以
只有一个极值,所以![]() 时,拉链长最短.下面比较
时,拉链长最短.下面比较![]() 与
与![]() 的大小
的大小![]() (其中
(其中![]() ),即
),即![]() ,亦即得
,亦即得![]()
![]() ,所以
,所以![]() 点的位置将下移.
点的位置将下移.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】不等式|sin x+tan x|<a的解集为N,不等式|sin x|+|tan x|<a的解集为M,则解集M与N的关系是( )
A. NM B. MN C. M=N D. MN
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 与过点
与过点![]() 且斜率为
且斜率为![]() 的直线交于
的直线交于![]() 两点.
两点.
(1)若线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值;
的值;
(2)在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使得
,使得![]() 的值为常数,若存在,求出点
的值为常数,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P:2+2=5,Q:3>2 ,则下列判断正确的是 ( ▲ )
A. “P或Q”为假,“非Q”为假 B. “P或Q”为真,“非Q”为假
C. “P且Q”为假,“非P”为假 D. “P且Q”为真,“P或Q”为假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一射手对靶射击,直到第一次命中为止每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目ξ的期望为
A. 2.44 B. 3.376 C. 2.376 D. 2.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() 图象与
图象与![]() 轴交于点
轴交于点![]() (
(![]() 异于原点),
异于原点),![]() 在
在![]() 处的切线为
处的切线为![]() ,
,![]() 图象与
图象与![]() 轴交于点
轴交于点![]() 且在该点处的切线为
且在该点处的切线为![]() ,并且
,并且![]() 与
与![]() 平行.
平行.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)已知实数![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(Ⅲ)令![]() ,给定
,给定![]() ,对于两个大于1的正数
,对于两个大于1的正数![]() ,存在实数
,存在实数![]() 满足:
满足:![]() ,
,![]() ,并且使得不等式
,并且使得不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一件产品要经过2道独立的加工程序,第一道工序的次品率为a,第二道工序的次品率为b,则产品的正品率为( )
A. 1-a-b B. 1-ab C. (1-a)(1-b) D. 1-(1-a)(1-b)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位拟采用系统抽样法对200名职工进行年龄调查,现将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com