
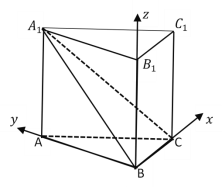
【题目】如图,在直三棱柱![]() 中,平面
中,平面![]() 侧面
侧面![]() ,且
,且![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,求锐二面角
,求锐二面角![]() 的大小.
的大小.
【答案】(1)证明过程详见解析;(2)![]()
【解析】
(1)连接![]() ,由已知可得四边形
,由已知可得四边形![]() 为正方形,则有
为正方形,则有![]() ,由面面垂直可证
,由面面垂直可证![]() 平面
平面![]() ,再证
,再证![]() 平面
平面![]() ,即可得证结论.
,即可得证结论.
(2)建立空间直角坐标系,利用空间向量坐标运算求出二面角的余弦值,即可求得答案.

(1)如图,连接![]()
因为在直三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,所以四边形
,所以四边形![]() 为正方形,
为正方形,
所以![]() ,又因为平面
,又因为平面![]() 侧面
侧面![]()
平面![]() 侧面
侧面![]() ,且
,且![]() 侧面
侧面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
又由![]() 平面
平面![]() 可得
可得![]() ,且
,且![]() ,
,
所以 ![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)由(1)知,![]() 平面
平面![]() ,
,![]()
如图,以![]() 为原点,以
为原点,以![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,
![]() 轴的正向建立空间直角坐标系.
轴的正向建立空间直角坐标系.
因为![]() ,
,![]() ,
,
则有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]()
设向量![]() 是平面
是平面![]() 的法向量,
的法向量,
则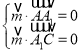 ,所以
,所以 ,
,
取![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
设向量![]() 是平面
是平面![]() 的法向量,
的法向量,
则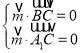 ,所以
,所以 ,
,
取![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
因为![]() ,
,
设锐二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ,
,
所以![]() ,所以锐二面角
,所以锐二面角![]() 的大小为
的大小为![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种,
方案一:每满200元减50元;
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、l个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
(1)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(2)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 人站成两排队列,前排
人站成两排队列,前排![]() 人,后排
人,后排![]() 人.
人.
(1)一共有多少种站法;
(2)现将甲、乙、丙三人加入队列,前排加一人,后排加两人,其他人保持相对位置不变,求有多少种不同的加入方法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2.0)为其右焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在平行于OA的直线L,使得直线L与椭圆C有公共点,且直线OA与L的距离等于4?若存在,求出直线L的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习小组在研究性学习中,对昼夜温差大小与绿豆种子一天内出芽数之间的关系进行研究.该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的100颗绿豆种子当天内的出芽数(如图2).
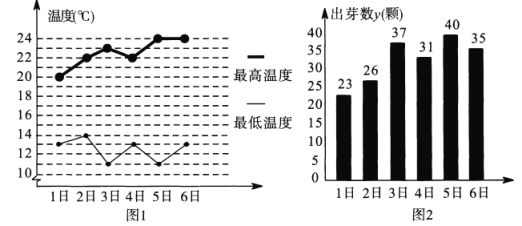
根据上述数据作出散点图,可知绿豆种子出芽数![]() (颗)和温差
(颗)和温差![]() (
(![]() )具有线性相关关系.
)具有线性相关关系.
(1)求绿豆种子出芽数![]() (颗)关于温差
(颗)关于温差![]() (
(![]() )的回归方程
)的回归方程![]() ;
;
(2)假如4月1日至7日的日温差的平均值为11![]() ,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
附: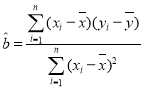
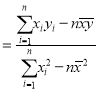 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() )图象上两个相邻的最值点为
)图象上两个相邻的最值点为![]() 和
和![]()
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在区间
在区间![]() 上的对称中心、对称轴;
上的对称中心、对称轴;
(3)将函数![]() 图象上每一个点向右平移
图象上每一个点向右平移![]() 个单位得到函数
个单位得到函数![]() ,令
,令![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值,并指出此时x的值.
上的最大值,并指出此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com