
【题目】已知二次函数f(x)=2x2﹣4x.
(1)指出图象的开口方向、对称轴方程、顶点坐标;
(2)用描点法画出它的图象;
(3)求出函数的最值,并分析函数的单调性.
【答案】
(1)解:二次函数f(x)=2x2﹣4x,
可化为f(x)=2(x﹣1)2﹣2,其图象的开口向上,
对称轴方程为x=1,顶点坐标为(1,﹣2)
(2)解:画出函数图象,如图示:
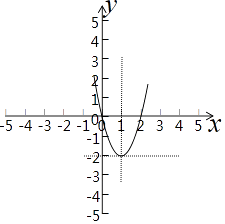
(3)解:当时x=1,二次函数f(x)=2x2﹣4x的最小值为﹣2;
当x>1时,函数是增加的,当x<1时,函数是减少的
【解析】(1)根据二次函数的解析式求出开口方向、对称轴方程、顶点坐标;(2)画出函数图象即可;(3)求出函数的最小值,得到函数的单调性即可.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】(1)已知一个圆过直线![]() 与圆
与圆![]() 的两个交点,且面积最小,求此圆的方程;
的两个交点,且面积最小,求此圆的方程;
(2)抛物线![]() 的顶点在原点,以椭圆
的顶点在原点,以椭圆![]() 的右焦点为焦点,过点
的右焦点为焦点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 有且仅有一个公共点,求直线
有且仅有一个公共点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+bx+c,若f(﹣3)=f(1),f(0)=﹣3.
(1)求函数f(x)的解析式;
(2)若函数g(x)= ![]() 画出函数g(x)图象;
画出函数g(x)图象;
(3)求函数g(x)在[﹣3,1]的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+2,
(1)求实数a的取值范围,使函数y=f(x)在区间[﹣5,5]上是单调函数;
(2)若x∈[﹣5,5],记y=f(x)的最大值为g(a),求g(a)的表达式并判断其奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
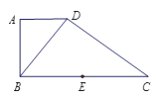
【题目】如图,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 点
, 点![]() 是
是![]() 边的中点, 将△
边的中点, 将△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() ,
, ![]() ,
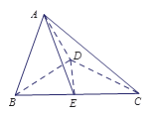
, ![]() , 得到如
, 得到如
图所示的空间几何体.
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,点 ![]() 的极坐标是
的极坐标是![]() ,曲线
,曲线 ![]() 的极坐标方程为
的极坐标方程为![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为 ![]() 轴的正半轴建立平面直角坐标系,斜率为
轴的正半轴建立平面直角坐标系,斜率为 ![]() 的直线
的直线 ![]() 经过点
经过点![]() .
.
(1)写出直线 ![]() 的参数方程和曲线
的参数方程和曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线 ![]() 和曲线
和曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙![]() :
: ![]() 与⊙
与⊙![]() :
: ![]() ,以
,以![]() ,
, ![]() 分别为左右焦点的椭圆
分别为左右焦点的椭圆![]() :
: ![]() 经过两圆的交点.
经过两圆的交点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左右顶点,
的左右顶点, ![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上非顶点的三点,若
上非顶点的三点,若![]() ∥
∥![]() ,
, ![]() ∥
∥![]() ,试问
,试问![]() 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com