
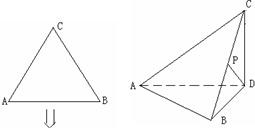
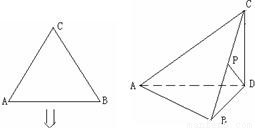
 把边长为2的正三角形ABC沿BC上的高AD折成直二面角,设折叠后BC的中点为P,
把边长为2的正三角形ABC沿BC上的高AD折成直二面角,设折叠后BC的中点为P,| AC |
| DP |
 解:(I)如图,以D为坐标原点,DB、AD、DC所在直线分别为x,y,z轴建立直角坐标系.则A(0,-
解:(I)如图,以D为坐标原点,DB、AD、DC所在直线分别为x,y,z轴建立直角坐标系.则A(0,-| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC |
| 3 |
| PD |
| 1 |
| 2 |
| 1 |
| 2 |
| AC |
| DP |
| ||||
|
|
| ||
| 4 |
| ||
| 4 |
| n1 |
| n2 |
|
|
| n2 |
| 3 |
| n1 |
| ||||
|
|
| ||
| 7 |
| ||
| 7 |


科目:高中数学 来源: 题型:
 已知l1,l2,l3是同一平面内三条不重合自上而下的平行直线.
已知l1,l2,l3是同一平面内三条不重合自上而下的平行直线.查看答案和解析>>
科目:高中数学 来源: 题型:
09年湖北鄂州5月模拟文)(12分)如图所示,将边长为2的正三角形铁皮的三个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正三棱柱容器,要求正三棱柱容器的高x与底面边长之比不超过正常数t.
⑴把正三棱柱容器的容积V表示为x的函数,并写出函数的定义域;
⑵x为何值时,容积V最大?并求最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知![]() 、
、![]() 、
、![]() 是同一平面内三条不重合自上而下的平行直线.
是同一平面内三条不重合自上而下的平行直线.
(Ⅰ)如果![]() 与
与![]() 间的距离是1,
间的距离是1,![]() 与
与![]() 间的距离也是1,可以把一个正三角形
间的距离也是1,可以把一个正三角形![]() 的三顶点分别放在
的三顶点分别放在![]() ,
,![]() ,
,![]() 上,求这个正三角形
上,求这个正三角形![]() 的边长;
的边长;
(Ⅱ)如图,如果![]() 与
与![]() 间的距离是1,
间的距离是1,![]() 与
与![]() 间的距离是2,能否把一个正三角形
间的距离是2,能否把一个正三角形![]() 的三顶点分别放在
的三顶点分别放在![]() ,
,![]() ,
,![]() 上,如果能放,求
上,如果能放,求![]() 和
和![]() 夹角的正切值并求该正三角形边长;如果不能,说明为什么?
夹角的正切值并求该正三角形边长;如果不能,说明为什么?
(Ⅲ)如果边长为2的正三角形![]() 的三顶点分别在
的三顶点分别在![]() ,
,![]() ,
,![]() 上,设
上,设![]() 与
与![]() 的距离为
的距离为![]() ,
,![]() 与
与![]() 的距离为
的距离为![]() ,求
,求![]() 的范围?
的范围?

查看答案和解析>>
科目:高中数学 来源:2008年湖南省高考数学试卷(单独招生)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com