
【题目】设集合A={x|x+2<0},B={x|(x+3)(x﹣1)>0}.
(1)求集合A∩B;
(2)若不等式ax2+2x+b>0的解集为A∪B,求a,b的值.
【答案】
(1)解:集合A={x|x+2<0}=(﹣∞,﹣2),B={x|(x+3)(x﹣1)>0}=(﹣∞,﹣3)∪(1,+∞),
∴A∩B=(﹣∞,﹣3)
(2)解:由(1)可求A∪B=(﹣∞,﹣2)∪(1,+∞),
∴﹣2,1为方程ax2+2x+b=0的两个根,且a>0,
∴﹣2+1=﹣ ![]() ,﹣2×1=
,﹣2×1= ![]() ,
,
解得a=2,b=﹣4
【解析】(1)化集合A,B,即可确定出两集合的交集;(2)确定出两集合的并集,由不等式ax2+2x+b>0的解集为两集合的并集,得到方程ax2+2x+b=0的两根分别为﹣2和1,利用根与系数的关系即可求出a与b的值.
【考点精析】通过灵活运用集合的交集运算,掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立即可以解答此题.
B,反之也成立即可以解答此题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,甲船以每小时15 ![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里,当甲船航行40分钟到达A2处时,乙船航行到甲船的南偏西45°方向的B2处,此时两船相距10海里,问乙船每小时航行多少海里?
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里,当甲船航行40分钟到达A2处时,乙船航行到甲船的南偏西45°方向的B2处,此时两船相距10海里,问乙船每小时航行多少海里? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意 ![]() 都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处。
海里处。
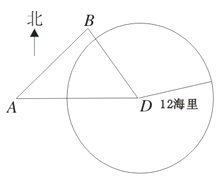
(Ⅰ)求此时该外国船只与![]() 岛的距离;
岛的距离;
(Ⅱ)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方向航行。为了将该船拦截在离
海里的速度沿正南方向航行。为了将该船拦截在离![]() 岛
岛![]() 海里处,不让其进入
海里处,不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值.
海里内的海域,试确定海监船的航向,并求其速度的最小值.
(参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos(x+ ![]() )[sin(x+
)[sin(x+ ![]() )﹣
)﹣ ![]() cos(x+
cos(x+ ![]() )].
)].
(1)求f(x)的值域和最小正周期;
(2)若对任意x∈[0, ![]() ],[f(x)+
],[f(x)+ ![]() ]﹣2m=0成立,求实数m的取值范围.
]﹣2m=0成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面区域D由以A(2,4)、B(5,2)、C(3,1)为顶点的三角形内部和边界组成,若在区域D上有无穷多个点(x,y)可使目标函数z=x+my取得最小值,则m= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+1)x+1(a∈R).
(1)若关于x的不等式f(x)≥0的解集为R,求实数a的取值范围;
(2)若关于x的不等式f(x)<0的解集是{x|b<x<2},求a,b的值;
(3)若关于x的不等式f(x)≤0的解集是 P,集合Q={x|0≤x≤1},若 P∩Q=,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为2,前n项和为Sn , 且 ![]() ﹣
﹣ ![]() =
= ![]() (n∈N*).
(n∈N*).
(1)求a2的值;
(2)设bn= ![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)若am , ap , ar(m,p,r∈N* , m<p<r)成等比数列,试比较p2与mr的大小,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( ) 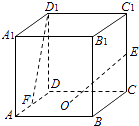
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com