
【题目】设函数![]() ,其中
,其中![]() ,
,![]() 是自然对数的底数.
是自然对数的底数.
(1)若![]() 在
在![]() 上存在两个极值点,求
上存在两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() ,证明:
,证明:![]() .
.
【答案】(1) ![]() (2)见证明
(2)见证明
【解析】
(1)![]() 在
在![]() 上存在两个极值点等价于
上存在两个极值点等价于![]() 在
在![]() 有两个根,分离参数
有两个根,分离参数![]() ,分析函数
,分析函数![]() 的单调性及极值,即可得出
的单调性及极值,即可得出![]() 取值;
取值;
范围.(2)![]() 即
即![]() ,等价于
,等价于![]() ,令
,令![]() ,利用导数求函数的最值,证明最大值小于0即可.
,利用导数求函数的最值,证明最大值小于0即可.
(1)由题意可知,![]() ,
,![]() ,
,
![]() 在
在![]() 上存在两个极值点等价于
上存在两个极值点等价于![]() 在
在![]() 有两个根,
有两个根,
由![]() 可得,
可得,![]() ,令
,令![]() ,
,
则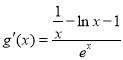 ,令
,令![]() ,
,
可得![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
所以![]() 是
是![]() 的极大值也是最大值,又当
的极大值也是最大值,又当![]() ,当
,当![]() 大于
大于![]() 趋向于
趋向于![]() ,
,
要使![]() 在
在![]() 有两个根,只需
有两个根,只需![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() ;
;
(2)证明:![]() 即
即![]() ,等价于
,等价于![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,单调递增,所以
,单调递增,所以![]() ,
,
当![]() 时,
时,![]() ,令
,令![]() ,
,
![]() ,又
,又![]() ,
,
取![]() ,且使
,且使![]() ,即
,即![]() ,
,
则有![]() ,
,
因为![]() ,故
,故![]() 存在唯一零点
存在唯一零点![]() ,
,
即![]() 有唯一的极值点且为极小值点
有唯一的极值点且为极小值点![]() ,
,
由![]() 可得,
可得,![]() ,故
,故![]() ,
,
因为![]() ,故
,故![]() 为
为![]() 上的增函数,
上的增函数,
所以![]()
![]() ,所以
,所以![]() .
.
综上,当![]() 时,总有
时,总有![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某市教育局卫生健康所对全市高三年级的学生身高进行抽样调查,随机抽取了100名学生,他们身高都处于![]() 五个层次,根据抽样结果得到如下统计图表,则从图表中不能得出的信息是( )
五个层次,根据抽样结果得到如下统计图表,则从图表中不能得出的信息是( )
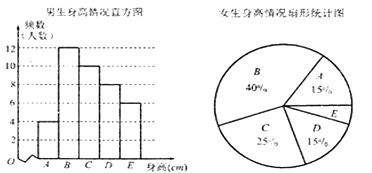
A. 样本中男生人数少于女生人数
B. 样本中![]() 层次身高人数最多
层次身高人数最多
C. 样本中![]() 层次身高的男生多于女生
层次身高的男生多于女生
D. 样本中![]() 层次身高的女生有3人
层次身高的女生有3人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查煤矿公司员工的饮食习惯与月收入之间的关系,随机抽取了30名员工,并制作了这30人的月平均收入的频率分布直方图和饮食指数表(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).其中月收入4000元以上员工中有11人饮食指数高于70.
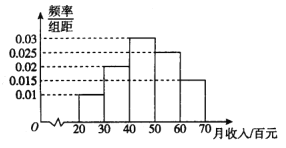
20 | 21 | 21 | 25 | 32 | 33 |
36 | 37 | 42 | 43 | 44 | 45 |
45 | 58 | 58 | 59 | 61 | 66 |
74 | 75 | 76 | 77 | 77 | 78 |
78 | 82 | 83 | 85 | 86 | 90 |
(Ⅰ)是否有95%的把握认为饮食习惯与月收入有关系?若有请说明理由,若没有,说明理由并分析原因;
(Ⅱ)以样本中的频率作为概率,从该公司所有主食蔬菜的员工中随机抽取3人,这3人中月收入4000元以上的人数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(Ⅲ)经调查该煤矿公司若干户家庭的年收入![]() (万元)和年饮食支出
(万元)和年饮食支出![]() (万元)具有线性相关关系,并得到
(万元)具有线性相关关系,并得到![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:![]() .若该公司一个员工与其妻子的月收入恰好都为这30人的月平均收入(该家庭只有两人收入),估计该家庭的年饮食支出费用.
.若该公司一个员工与其妻子的月收入恰好都为这30人的月平均收入(该家庭只有两人收入),估计该家庭的年饮食支出费用.
附:
![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,
,![]() 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.

(1)从![]() 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;
(2)在半圆内任取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到![]() 地区用户满意度评分的频率分布直方图和
地区用户满意度评分的频率分布直方图和![]() 地区用户满意度评分的频数分布表.
地区用户满意度评分的频数分布表.
![]() 地区用户满意度评分的频率分布直方图
地区用户满意度评分的频率分布直方图
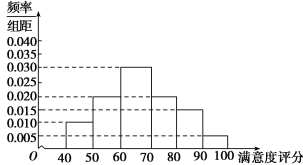
![]() 地区用户满意度评分的频数分布表
地区用户满意度评分的频数分布表
满意度评分分组 |
|
|
|
|
|
频数 | 2 | 8 | 14 | 10 | 6 |
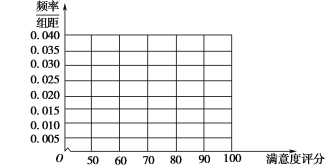
(1)在图中作出![]() 地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).
地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).
![]() 地区用户满意度评分的频率分布直方图
地区用户满意度评分的频率分布直方图
(2)根据用户满意度评分,将用户的满意度分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | td style="width:88.95pt; border-left-style:solid; border-left-width:0.75pt; border-bottom-style:solid; border-bottom-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">|
满意度等级 | 不满意 | 满意 | 非常满意 |
公司负责人为了解用户满意度情况,从![]() 地区中调查8户,其中有2户满意度等级是不满意,求从这8户中随机抽取2户检查,抽到不满意用户的概率.
地区中调查8户,其中有2户满意度等级是不满意,求从这8户中随机抽取2户检查,抽到不满意用户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() .我们将其结论推广:椭圆
.我们将其结论推广:椭圆![]() (
(![]() )上的点
)上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用.已知,直线
,在解本题时可以直接应用.已知,直线![]() 与椭圆
与椭圆![]() :
:![]() (
(![]() )有且只有一个公共点.
)有且只有一个公共点.
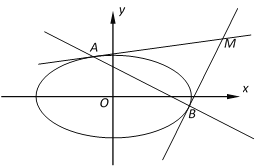
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .当
.当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)若![]() 是椭圆
是椭圆![]()
![]() 上不同的两点,
上不同的两点,![]()
![]() 轴,圆
轴,圆![]() 过
过![]() 且椭圆
且椭圆![]() 上任意一点都不在圆
上任意一点都不在圆![]() 内,则称圆
内,则称圆![]() 为该椭圆的一个内切圆.试问:椭圆
为该椭圆的一个内切圆.试问:椭圆![]() 是否存在过左焦点
是否存在过左焦点![]() 的内切圆?若存在,求出圆心
的内切圆?若存在,求出圆心![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com