
【题目】已知圆C的方程:x2+y2﹣4x﹣6y+m=0,若圆C与直线a:x+2y﹣3=0相交于M、N两点,且|MN|=2 ![]() .
.
(1)求m的值;
(2)是否存在直线l:x﹣y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围;若不存在,请说明理由.
,若存在,求出c的范围;若不存在,请说明理由.
【答案】
(1)解:方程x2+y2﹣4x﹣6y+m=0配方为(x﹣2)2+(y﹣3)2=13﹣m.
∵此方程表示圆,
∴13﹣m>0,即m<13.r= ![]() ,
,
圆C与直线a:x+2y﹣3=0相交于M、N两点,且|MN|=2 ![]() .
.
圆的圆心到直线的距离为:d= ![]() =
= ![]() .
.
可得 ![]() .
.
即:5=13﹣m﹣3,解得m=5
(2)解:(x﹣2)2+(y﹣3)2=8.圆的圆心(2,3),半径为2 ![]()
直线l:x﹣y+c=0,使得圆上有四点到直线l的距离为 ![]() ,
,
则圆心C(2,3)到直线l:x﹣y+c=0的距离为: ![]() =
= ![]() ,
,
可得:2 ![]() ﹣
﹣ ![]() >
> ![]() ,
,
解得﹣2<c<4
【解析】(1)由方程x2+y2﹣4x﹣6y+m=0配方为(x﹣2)2+(y﹣3)2=13﹣m.由于此方程表示圆,可得13﹣m>0,解出m的范围,利用弦心距与半径半弦长的关系,求解m即可.(2)求出圆心与半径,利用半径与圆的圆心到直线的距离的差大于 ![]() ,列出不等式求解即可.
,列出不等式求解即可.


科目:高中数学 来源: 题型:
【题目】如图是某市2017年3月1日至16日的空气质量指数趋势图,空气质量指数![]() 小于
小于![]() 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于![]() 表示空气重度污染.
表示空气重度污染.
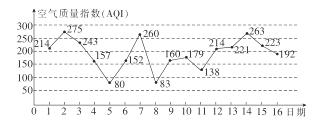
(1)若该人随机选择3月1日至3月14日中的某一天到达该市,到达后停留![]() 天(到达当日算
天(到达当日算![]() 天),求此人停留期间空气重度污染的天数为
天),求此人停留期间空气重度污染的天数为![]() 天的概率;
天的概率;
(2)若该人随机选择3月7日至3月12日中的![]() 天到达该市,求这
天到达该市,求这![]() 天中空气质量恰有
天中空气质量恰有![]() 天是重度污染的概率.
天是重度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3sin(2x+ ![]() )的图象为C,关于函数f(x)及其图象的判断如下: ①图象C关于点(
)的图象为C,关于函数f(x)及其图象的判断如下: ①图象C关于点( ![]() ,0)对称;
,0)对称;
②图象C关于直线x= ![]() 对称;
对称;
③由图象C向右平移 ![]() 个单位长度可以得到y=3sin2x的图象;
个单位长度可以得到y=3sin2x的图象;
④函数f(x)在区间(﹣ ![]() ,
, ![]() )内是减函数;
)内是减函数;
⑤函数|f(x)+1|的最小正周期为 ![]() .
.
其中正确的结论序号是 . (把你认为正确的结论序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 经过不同的三点
经过不同的三点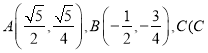 在第三象限),线段
在第三象限),线段![]() 的中点在直线
的中点在直线![]() 上.
上.
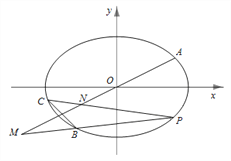
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设点![]() 是椭圆
是椭圆![]() 上的动点(异于点
上的动点(异于点![]() 且直线
且直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,问
两点,问![]() 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三角形ABC中,分别根据下列条件解三角形,其中有两个解的是( )
A.a=8b=16A=30°
B.a=25b=30A=150°
C.a=30b=40A=30°
D.a=72b=60A=135°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+y2=4
(1)求过点P(3,3)且与圆C相切的直线l的方程;
(2)已知直线m:x﹣y+1=0与圆C交于A、B两点,求|AB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com