
【题目】某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( ) 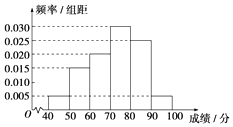
A.73.3,75,72
B.72,75,73.3
C.75,72,73.3
D.75,73.3,72
【答案】B
【解析】解:①平均数是频率分布直方图的“重心”,
等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
所以平均成绩为:
45×(0.005×10)+55×(0.015×10)+65×(0.020×10)+
75×(0.030×10)+85×(0.025×10)+95×(0.005×10)=72;
②由众数概念知,众数是出现次数最多的,
在直方图中,高度最高的小矩形的中间值的横坐标即为众数,
由频率分布直方图知,这次测试数学成绩的众数为75;
③由于中位数是所有数据中的中间值,
故在直方图中,体现的是中位数的左右两边频数应用相等,即频率相等,
从而就是小矩形的面积和相等,
因此在频率分布直方图中,
将频率分布直方图中所有小矩形面积一分为二的直线所对应的成绩即为所求,
∵前三个小矩形的面积和为(0.005+0.015+0.020)×10=0.4,
第四个小矩形的面积为0.030×10=0.3,0.4+0.3=0.7>0.5,
∴中位数应位于第四个小矩形中,
设其底边为x,高为0.03,
∴令0.03x=0.1,解得x≈3.3,
故成绩的中位数为73.3.
故选:B.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() a(x﹣1)(a∈R).
a(x﹣1)(a∈R).
(1)若a=﹣2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若不等式f(x)<0对任意x∈(1,+∞)恒成立. (ⅰ)求实数a的取值范围;
(ⅱ)试比较ea﹣2与ae﹣2的大小,并给出证明(e为自然对数的底数,e=2.71828).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AB=2BB1=2BC,E为D1C1的中点,连结ED,EC,EB和DB.
(Ⅰ)证明:A1D1∥平面EBC;
(Ⅱ)证明:平面EDB⊥平面EBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,a1=2,a4=16.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若a3 , a5分别为等差数列{bn}的第4项和第16项,试求数列{bn}的前项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个路口的红绿灯,红灯亮的时间为40秒,黄灯亮的时间为5秒,绿灯亮的时间为50秒(没有两灯同时亮),当你到达路口时,看见下列三种情况的概率各是多少?
(1)红灯;
(2)黄灯;
(3)不是红灯.
查看答案和解析>>
科目:高中数学 来源: 题型:
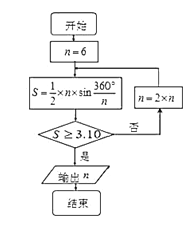
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出![]() 的值为 ( )
的值为 ( )
(参考数据:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com