
【题目】在直角坐标系xOy中,l是过定点P(4,2)且倾斜角为α的直线;在极坐标系(以坐标原点O为极点,
以x轴非负半轴为极轴,取相同单位长度)中,曲线C的极坐标方程为![]() .
.
(1)写出直线l的参数方程,并将曲线C的方程化为直角坐标方程;
(2)若曲线C与直线相交于不同的两点M,N,求|PM|+|PN|的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据![]() 直接写出
直接写出![]() 的参数方程,利用极坐标与直角坐标的转换关系式
的参数方程,利用极坐标与直角坐标的转换关系式![]() ,可将曲线C的方程化为直角坐标方程;(2)联立
,可将曲线C的方程化为直角坐标方程;(2)联立![]() 的参数方程与曲线
的参数方程与曲线![]() 的普通方程,消去
的普通方程,消去![]() 与
与![]() ,得到关于
,得到关于![]() 的一元二次方程,写出
的一元二次方程,写出![]() 关于
关于![]() 及
及![]() 的表达式,利用韦达定理及
的表达式,利用韦达定理及![]() 的范围,可探求
的范围,可探求![]() 的取值范围.
的取值范围.
试题解析:(1)直线l的参数方程为![]() (t为参数).
(t为参数).
∵ρ=4cos θ,∴ρ2=4ρcos θ,所以C:x2+y2=4x.
(2)直线l的参数方程为![]() (t为参数),代入C:x2+y2=4x,得
(t为参数),代入C:x2+y2=4x,得
t2+4(sin α+cos α)t+4=0,
则有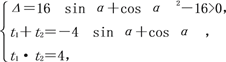 ∴sin α·cos α>0,又α∈[0,π),
∴sin α·cos α>0,又α∈[0,π),
所以α∈![]() ,t1<0,t2<0.
,t1<0,t2<0.
而|PM|+|PN|=![]() +
+
![]() =|t1|+|t2|
=|t1|+|t2|
=-t1-t2=4(sin α+cos α)=4![]() sin
sin![]() .
.
∵α∈![]() ,∴α+
,∴α+![]() ∈
∈![]() ,∴
,∴![]() <sin
<sin![]() ≤1,
≤1,
所以|PM|+|PN|的取值范围为(4,4![]() ].
].


科目:高中数学 来源: 题型:
【题目】如图(1),在等腰梯形![]() 中,
中, ![]() ,
, ![]() 是梯形的高,
是梯形的高, ![]() ,
, ![]() ,现将梯形沿
,现将梯形沿![]() ,
, ![]() 折起,使
折起,使![]() 且
且![]() ,得一简单组合体
,得一简单组合体![]() 如 图(2)示,已知
如 图(2)示,已知![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角大小.
所成的锐二面角大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-![]() (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图像与函数h(x)=![]() 的图像关于点A(0,1)对称。
的图像关于点A(0,1)对称。
(1)求函数f(x)的解析式;
(2)若g(x)=xf(x)+ax,且g(x)在区间(0,4]上为减函数,求实数a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com