
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是BC的中点. 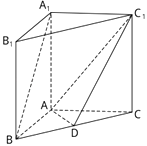
(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求几何体ABD﹣A1B1C1的体积.
【答案】
(1)证明:连接A1C,交AC1于点E,
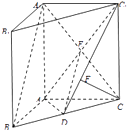
则点E是A1C及AC1的中点.
连接DE,则DE∥A1B.
因为DE平面ADC1,所以A1B∥平面ADC1
(2)解:∵AB⊥AC,AB=AC=1,AA1=2,
∴几何体ABD﹣A1B1C1的体积:
V= ![]() ﹣
﹣ ![]()
=S△ABC×AA1﹣ ![]()
= ![]() ﹣
﹣ ![]()
=1﹣ ![]() =
= ![]() .
.
【解析】(1)连接A1C,交AC1于点E,连接DE,则DE∥A1B.由此能证明A1B∥平面ADC1 . (2)几何体ABD﹣A1B1C1的体积V= ![]() ﹣
﹣ ![]() ,由此能求出结果.
,由此能求出结果.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=bax(a>0,且a≠1,b∈R)的图象经过点A(1,6),B(3,24).
(1)设g(x)= ![]() ﹣
﹣ ![]() ,确定函数g(x)的奇偶性;
,确定函数g(x)的奇偶性;
(2)若对任意x∈(﹣∞,1],不等式( ![]() )x≥2m+1恒成立,求实数m的取值范围.
)x≥2m+1恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
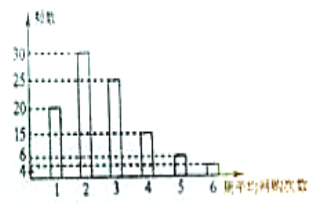
(1)根据已知条件完成下面的![]() 列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
网购迷 | 非网购迷 | 合计 | |
年龄不超过40岁 | |||
年龄超过40岁 | |||
合计 |
(2)若从网购迷中任意选取2名,求其中年龄超过40岁的市民人数![]() 的分布列与期望.
的分布列与期望.
附: 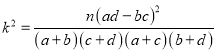 ;
;
| 0.15 | 0.10 | 0.05 | 0.01 |
| 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°. 
(1)求证:平面PBD⊥平面PAC;
(2)求点A到平面PBD的距离;
(3)求二面角A﹣PB﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣1,1),则函数g(x)=f( ![]() )+f(x﹣1)的定义域为( )
)+f(x﹣1)的定义域为( )
A.(﹣2,0)
B.(﹣2,2)
C.(0,2)
D.(﹣ ![]() ,0)
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com