
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 为菱形, 且
为菱形, 且![]() 是
是![]() 的中点.
的中点.
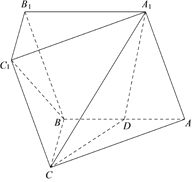
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是______
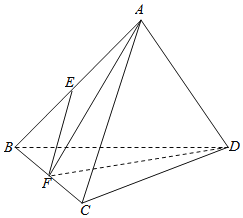
①异面直线AB与CD所成角为90°;
②直线AB与平面BCD所成角为60°;
③直线EF∥平面ACD
④平面AFD⊥平面BCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() 为等腰三角形,
为等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线
是两条不同的直线![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:(1)若
是三个不同的平面,给出下列四个命题:(1)若![]() ,
,![]() ,那么
,那么![]() ;(2)若
;(2)若![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;(3)若
;(3)若![]() ,
,![]() ,那么
,那么![]() ;(4)若
;(4)若![]() ,
,![]() ,则
,则![]() ,其中正确命题的序号是( )
,其中正确命题的序号是( )
A.(1)(2)B.(2)(3)C.(1)(3)D.(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(
,(![]() 为常数)
为常数)
(1)若![]()
①求函数![]() 在区间
在区间![]() 上的最大值及最小值。
上的最大值及最小值。
②若过点![]() 可作函数
可作函数![]() 的三条不同的切线,求实数
的三条不同的切线,求实数![]() 的取值范围。
的取值范围。
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=![]() ,M为BC的中点.
,M为BC的中点.
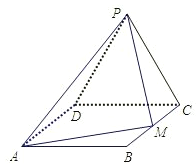
(I)证明:AM⊥PM ;
(II)求二面角P-AM-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了考察某校高三年级的教学水平,将抽查这个学校高三年级部分学生本学年的考试成绩.已知该校高三年级共有14个班,假定该校每班人数都相同.为了全面地反映实际情况,采取以下两种方法进行抽查:①从全年级14个班中任意抽取一个班,再从该班中任意抽取14人,考察他们的成绩;②把该校高三年级的学生按成绩分成优秀、良好、普通三个级别,从中抽取100名学生进行考察(已知若按成绩分层,该校高三学生中优秀学生有105名,良好学生有420名,普通学生有175名).根据上面的叙述,试回答下列问题:
(1)以上调查各自采用的是什么抽样方法?
(2)试分别写出上面两种抽样方法各自抽取样本的步骤.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com