
【题目】已知函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围.
(2)当a∈[4,6]时,f(x)≥0恒成立,求x的取值范围.
【答案】(1)-6≤a≤2; (2){x|x≤-3-![]() 或x≥-3+
或x≥-3+![]() }
}
【解析】
(1)f(x)≥a恒成立,x2+ax+3-a≥0对任意x∈R恒成立,根据判别式进而求解;
(2)设g(a)=x2+ax+3,转化成关于a的一次函数,进而求解.
解:(1)∵函数f(x)=x2+ax+3,当x∈R时,f(x)≥a恒成立,
∴x2+ax+3-a≥0对任意x∈R恒成立,
∴△=a2-4(3-a)≤0,
化简得a2+4a-12≤0,
解得:-6≤a≤2;
(2)设g(a)=x2+ax+3,
则由题可得:当a∈[4,6]时,恒有g(a)≥0,
∴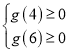 即
即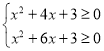 解得
解得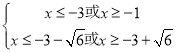 ,
,
即x≤-3-![]() 或x≥-3+
或x≥-3+![]() ,
,
∴x的取值范围是{x|x≤-3-![]() 或x≥-3+
或x≥-3+![]() }.
}.


科目:高中数学 来源: 题型:
【题目】已知直线l:y=kx+m与椭圆![]() +
+![]() =1(a>b>0)恰有一个公共点P,l与圆x2+y2=a2相交于A,B两点.
=1(a>b>0)恰有一个公共点P,l与圆x2+y2=a2相交于A,B两点.
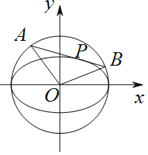
(Ⅰ)求m(用a,b,k表示);
(Ⅱ)当k=-![]() 时,△AOB的面积的最大值为
时,△AOB的面积的最大值为![]() a2,求椭圆的离心率.
a2,求椭圆的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知数列![]() 中,
中,![]() ,前项和
,前项和![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列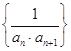 的前项和为
的前项和为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对一切正整数都成立?若存在,求出
对一切正整数都成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).

(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为全面贯彻党的教育方针,坚持立德树人,适应经济社会发展对多样化高素质人才的需要,按照国家统一部署,湖南省高考改革方案从2018年秋季进入高一年级的学生开始正式实施.新高考改革中,明确高考考试科目由语文、数学、英语![]() 科,及考生在思想政治、历史、地理、物理、化学、生物
科,及考生在思想政治、历史、地理、物理、化学、生物![]() 个科目中自主选择的
个科目中自主选择的![]() 科组成,不分文理科.假设
科组成,不分文理科.假设![]() 个自主选择的科目中每科被选择的可能性相等,每位学生选择每个科目互不影响,甲、乙、丙为某中学高一年级的
个自主选择的科目中每科被选择的可能性相等,每位学生选择每个科目互不影响,甲、乙、丙为某中学高一年级的![]() 名学生.
名学生.
(1)求这![]() 名学生都选择了物理的概率.
名学生都选择了物理的概率.
(2)设![]() 为这
为这![]() 名学生中选择物理的人数,求
名学生中选择物理的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() (n∈N*).
(n∈N*).
(1)证明数列![]() 是等比数列,求出数列
是等比数列,求出数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)数列![]() 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地棚户区改造建筑平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域近似为圆面,该圆面的内接四边形![]() 是原棚户区建筑用地,测量可知边界
是原棚户区建筑用地,测量可知边界![]() 万米,
万米,![]() 万米,
万米,![]() 万米.
万米.
(1)请计算原棚户区建筑用地![]() 的面积及
的面积及![]() 的长;
的长;
(2)因地理条件的限制,边界![]() 不能更改,而边界
不能更改,而边界![]() 可以调整,为了提高棚户区建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区建筑用地的利用率,请在圆弧![]() 上设计一点
上设计一点![]() ,使得棚户区改造后的新建筑用地
,使得棚户区改造后的新建筑用地![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com