
【题目】设函数![]()
(1)研究函数![]() 的极值点;
的极值点;
(2)当p>0时,若对任意的x>0,恒有![]() ,求p的取值范围;
,求p的取值范围;
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:
【题目】从全校参加科技知识竞赛初赛的学生试卷中,抽取一个样本,考察竞赛的成绩分布.将样本分成5组,绘成频率分布直方图(如图),图中从左到右各小组的小长方形的高之比是![]() ,最后一组的频数是6.请结合频率分布直方图提供的信息,解答下列问题:
,最后一组的频数是6.请结合频率分布直方图提供的信息,解答下列问题:
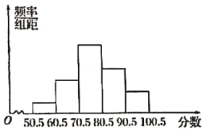
(1)样本的容量是多少?
(2)求样本中成绩在![]() 分的学生人数;
分的学生人数;
(3)从样本中成绩在90.5分以上的同学中随机地抽取2人参加决赛,求最高分甲被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个比赛安排4名志愿者完成6项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式有多少种( )
A.7200种B.4800种C.2640种D.1560种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某街道居委会拟在![]() 地段的居民楼正南方向的空白地段
地段的居民楼正南方向的空白地段![]() 上建一个活动中心,其中
上建一个活动中心,其中![]() 米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形
米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形![]() ,上部分是以
,上部分是以![]() 为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长
为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长![]() 不超过
不超过![]() 米,其中该太阳光线与水平线的夹角
米,其中该太阳光线与水平线的夹角![]() 满足
满足![]() .
.

(1)若设计![]() 米,
米,![]() 米,问能否保证上述采光要求?
米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计![]() 与
与![]() 的长度,可使得活动中心的截面面积最大?(注:计算中
的长度,可使得活动中心的截面面积最大?(注:计算中![]() 取3)
取3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某汽车品牌一个月内被消费者投诉的次数用![]() 表示,据统计,随机变量
表示,据统计,随机变量![]() 的概率分布如下:
的概率分布如下:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
(1)求![]() 的值;
的值;
(2)若每个月被消费者投诉的次数互不影响,求该汽车品牌在五个月内被消费者投诉3次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com