
【题目】将函数f(x)=sin(2x+ ![]() )图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移
)图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移 ![]() 个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
A.(﹣ ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.(﹣ ![]() ,0)
,0)
D.( ![]() ,0)
,0)
【答案】D
【解析】解:将函数f(x)=sin(2x+ ![]() )图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,可得y=sin(4x+
)图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,可得y=sin(4x+ ![]() )的图象;
)的图象;
再将所得图象向左平移 ![]() 个单位得到函数g(x)=sin(4x+
个单位得到函数g(x)=sin(4x+ ![]() +
+ ![]() )=sin(4x+
)=sin(4x+ ![]() )的图象.
)的图象.
令4x+ ![]() =kπ,求得x=
=kπ,求得x= ![]() ﹣
﹣ ![]() ,k∈Z,令k=1,
,k∈Z,令k=1,
可得在g(x)图象的所有对称中心中,离原点最近的对称中心为( ![]() ,0),
,0),
所以答案是:D.
【考点精析】认真审题,首先需要了解函数y=Asin(ωx+φ)的图象变换(图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象).
的图象).


科目:高中数学 来源: 题型:
【题目】某种商品价格与该商品日需求量之间的几组对照数据如表:
价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程 ![]() ,其中
,其中 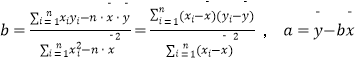 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=1,前n项和为Sn , 且满足(n+1)an=2Sn(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=ancos(πan),求数列{bn)的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方体ABCD﹣A1B1C1D1中,底面ABCD为正方形,DD1⊥平面ABCD,AB=4,AA1=2,点E1在棱C1D1上,且D1E1=3.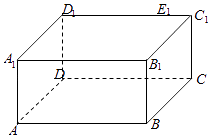
(Ⅰ)在棱CD上确定一点E,使得直线EE1∥平面D1DB,并写出证明过程;
(Ⅱ)若动点F在正方形ABCD内,且AF=2,请说明点F的轨迹,探求E1F长度的最小值并求此时直线E1F与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且an是2与Sn的等差中项.
(1)求数列{an}的通项公式;
(2)若 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com