
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
. 
(1)求证:AB⊥PC;
(2)求侧面BPC与侧面DPC所成的锐二面角的余弦值.
【答案】
(1)证明:取AB的中点O,连结PO,CO,AC,
∵△APB为等腰三角形,∴PO⊥AB,
又∵四边形ABCD是菱形,∠BCD=120°,
∴△ABC是等边三角形,∴CO⊥AB,
又OC∩PO=O,∴AB⊥平面PCO,
又PC平面PCO,∴AB⊥PC
(2)解:∵四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() ,
,
∴OP= ![]() =1,OC=
=1,OC= ![]() =
= ![]() ,∴PC2=OP2+OC2,∴OP⊥OC,
,∴PC2=OP2+OC2,∴OP⊥OC,
以O为原点,OC为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,
则B(0,1,0),C( ![]() ,0,0),P(0,0,1),D(
,0,0),P(0,0,1),D( ![]() ),
),
![]() =(
=( ![]() ),
), ![]() =(0,﹣1,1),
=(0,﹣1,1), ![]() =(
=( ![]() ,﹣1),
,﹣1),
设 ![]() =(x,y,z)是平面BPC的一个法向量,
=(x,y,z)是平面BPC的一个法向量,
则  ,取x=1,得
,取x=1,得 ![]() =(1,
=(1, ![]() ),
),
设平面DPC的一个法向量 ![]() =(a,b,c),
=(a,b,c),
则 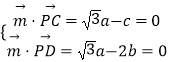 ,取a=1,得
,取a=1,得 ![]() =(1,0,
=(1,0, ![]() ),
),
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
∴侧面BPC与侧面DPC所成的锐二面角的余弦值为 ![]() .
.

【解析】(1)取AB的中点O,连结PO,CO,AC,推导出PO⊥AB,CO⊥AB,从而AB⊥平面PCO,由此能证明AB⊥PC.(2)以O为原点,OC为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出侧面BPC与侧面DPC所成的锐二面角的余弦值.
【考点精析】关于本题考查的空间中直线与直线之间的位置关系,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】己知在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数)以
为参数)以![]() 轴为极轴,
轴为极轴, ![]() 为极点建立极坐标系,在该极坐标系下,圆
为极点建立极坐标系,在该极坐标系下,圆![]() 是以点
是以点![]() 为圆心,且过点
为圆心,且过点![]() 的圆心.
的圆心.
(1)求圆![]() 及圆
及圆![]() 在平而直角坐标系
在平而直角坐标系![]() 下的直角坐标方程;
下的直角坐标方程;
(2)求圆![]() 上任一点
上任一点![]() 与圆
与圆![]() 上任一点之间距离的最小值.
上任一点之间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两运动员进行射击训练.已知他们击中的环数都稳定在![]() ,
,![]() ,
,![]() 环,且每次射击击中与否互不影响.甲、乙射击命中环数的概率如下表:
环,且每次射击击中与否互不影响.甲、乙射击命中环数的概率如下表:

(![]() )若甲、乙两运动员各射击
)若甲、乙两运动员各射击![]() 次,求甲运动员击中
次,求甲运动员击中![]() 环且乙运动员击中
环且乙运动员击中![]() 环的概率.
环的概率.
(![]() )若甲射击
)若甲射击![]() 次,用
次,用![]() 表示这
表示这![]() 次射击击中
次射击击中![]() 环以上(含
环以上(含![]() 环)的次数,求随机变量
环)的次数,求随机变量![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,∠BCA=90°,M、N分别是A1B1、A1C1的中点,BC=AC=CC1 , 则CN与AM所成角的余弦值等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() (
(![]() 位于第一象限)两点.
位于第一象限)两点.
(1)若直线![]() 的斜率为
的斜率为![]() ,过点
,过点![]() 分别作直线
分别作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(2)若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位安排![]() 位员工在春节期间大年初一到初七值班,每人值班
位员工在春节期间大年初一到初七值班,每人值班![]() 天,若
天,若![]() 位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有( )
位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点F. 
(1)证明:PB∥平面AEC;
(2)若ABCD为正方形,探究在什么条件下,二面角C﹣AF﹣D大小为60°?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com