
【题目】已知(![]() +3x2)n的展开式中,各项系数和比它的二项式系数和大992,求:
+3x2)n的展开式中,各项系数和比它的二项式系数和大992,求:
(1)展开式中二项式系数最大的项;
(2)展开式中系数最大的项.
【答案】
(1)
解:令x=1,则展开式中各项系数和为(1+3)n=22n.
又展开式中二项式系数和为2n,
∴22n-2n=992,n=5
∵n=5,展开式共6项,二项式系数最大的项为第3、4两项,∴T3= C52 ( ![]() )3(3x2)2=90x6,T4= C53 (
)3(3x2)2=90x6,T4= C53 ( ![]() )2(3x2)3=
)2(3x2)3=![]()
(2)
解:设展开式中第r+1项系数最大,
则Tr+1=C5r ( ![]() )5-r(3x2)r=3r C5r
)5-r(3x2)r=3r C5r![]() ,
,
∴ 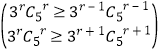 ,则
,则![]() ,∴r=4,
,∴r=4,
即展开式中第5项系数最大,T5= C54 ( ![]() )(3x2)4=405
)(3x2)4=405![]() .
.
【解析】本题主要考查了二项式系数的性质,解决问题的关键是(1)利用赋值法求出各项系数和,与二项式系数和求出 ![]() 值,利用二项式系数的性质求展开式中二项式系数最大的项;(2)设出展开式中系数最大的项,利用
值,利用二项式系数的性质求展开式中二项式系数最大的项;(2)设出展开式中系数最大的项,利用 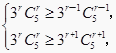 进行求解即可.
进行求解即可.


科目:高中数学 来源: 题型:
【题目】设函数y=x3与y=( ![]() )x﹣2的图象的交点为(x0 , y0),则x0所在的区间是( )
)x﹣2的图象的交点为(x0 , y0),则x0所在的区间是( )
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(3x+ ![]() )的图象,只需要把函数y=sin(x+
)的图象,只需要把函数y=sin(x+ ![]() )的图象上的所有点( )
)的图象上的所有点( )
A.横坐标伸长为原来的3倍,纵坐标不变
B.横坐标缩短为原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
C.纵坐标伸长为原来的3倍,横坐标不变
D.纵坐标缩短为原来的 ![]() 倍,横坐标不变
倍,横坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义域为R的函数 ![]() (a,b为实数).
(a,b为实数).
(1)若f(x)是奇函数,求a,b的值;
(2)当f(x)是奇函数时,证明对任何实数x,c都有f(x)<c2﹣3c+3成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】工人在安装一个正六边形零件时,需要固定如图所示的六个位置的螺丝,第一阶段,首先随意拧一个螺丝,接着拧它对角线上(距离它最远的,下同)螺丝,再随意拧第三个螺丝,第四个也拧它对角线上螺丝,第五个和第六个以此类推,但每个螺丝都不要拧死;第二阶段,将每个螺丝拧死,但不能连续拧相邻的2个螺丝。则不同的固定方式有 . 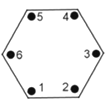
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的10%进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按2log5(A+1)进行奖励,没超出部分仍按销售利润的10%进行奖励.记奖金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员的奖励方案的函数表达式;
(2)如果业务员老张获得5.5万元的奖金,那么他的销售利润是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com