
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有 ![]() .
.
(1)解不等式 ![]() ;
;
(2)若f(x)≤t2﹣2at+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.
【答案】
(1)解:任取x1,x2∈[﹣1,1]且x1<x2,则 ![]()
∴f(x2)>f(x1),∴f(x)为增函数
∵ ![]()
∴ 
∴ ![]() ,
,
即不等式 ![]() 的解集为
的解集为 ![]()
(2)解:由于f(x)为增函数,∴f(x)的最大值为f(1)=1,
∴f(x)≤t2﹣2at+1对x∈[﹣1,1],a∈[﹣1,1]恒成立,等价于t2﹣2at+1≥1对任意的a∈[﹣1,1]恒成立,
即t2﹣2at≥0对任意的a∈[﹣1,1]恒成立.
把y=t2﹣2at看作a的函数,由于a∈[﹣1,1]知其图象是一条线段.
∵t2﹣2at≥0对任意的a∈[﹣1,1]恒成立
∴ ![]()
∴ ![]()
解得t≤﹣2或t=0或t≥2
【解析】(1)由f(x)是奇函数和单调性的定义,可得f(x)在[﹣1,1]上是增函数,再利用定义的逆用求解;(2)先由(1)求得f(x)的最大值,再转化为关于a的不等式恒成立问题求解.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】如图是在竖直平面内的一个“通道游戏”,图中竖直线段和斜线段都表示通道,并且在交点处相通,假设一个小弹子在交点处向左或向右是等可能的.若竖直线段有一条的为第一层,有两条的为第二层,……,依此类推,现有一颗小弹子从第一层的通道里向下运动.则该小弹子落入第四层从左向右数第3个竖直通道的概率是( )
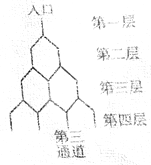
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 曲线
曲线![]() 在原点处的切线为
在原点处的切线为![]() .
.
(1)证明:曲线![]() 与
与![]() 轴正半轴有交点;
轴正半轴有交点;
(2)设曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,曲线在点
,曲线在点![]() 处的切线为直线
处的切线为直线![]() ,求证:曲线
,求证:曲线![]() 上的点都不在直线
上的点都不在直线![]() 的上方 ;
的上方 ;
(3)若关于![]() 的方程
的方程![]() (
(![]() 为正实数)有不等实根
为正实数)有不等实根![]() 求证:
求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
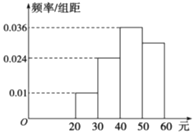
【题目】某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在![]() 元的学生有60人,则下列说法正确的是______.
元的学生有60人,则下列说法正确的是______.
A.样本中支出在![]() 元的频率为
元的频率为![]()
B.样本中支出不少于40元的人数有132
C.n的值为200
D.若该校有2000名学生,则定有600人支出在![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查,某地区有300万从事传统农业的农民,人均年收入6000元,为了增加农民的收入,当地政府积极引进资本,建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有![]() 万人进企业工作,那么剩下从事传统农业的农民的人均年收入有望提高
万人进企业工作,那么剩下从事传统农业的农民的人均年收入有望提高![]() ,而进入企业工作的农民的人均年收入为
,而进入企业工作的农民的人均年收入为![]() 元.
元.
(1)在建立加工企业后,多少农民进入企业工作,能够使剩下从事传统农业农民的总收入最大,并求出最大值;
(2)为了保证传统农业的顺利进行,限制农民加入加工企业的人数不能超过总人数的![]() ,当地政府如何引导农民,即
,当地政府如何引导农民,即![]() 取何值时,能使300万农民的年总收入最大.
取何值时,能使300万农民的年总收入最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将现有![]() 名男生和
名男生和![]() 名女生站成一排照相.(用数字作答)
名女生站成一排照相.(用数字作答)
(1)两女生相邻,有多少种不同的站法?
(2)两名女生不相邻,有多少种不同的站法?
(3)女生甲不在左端,女生乙不在右端,有多少种不同的站法?
(4)女生甲要在女生乙的右方(可以不相邻)有多少种不同的站法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数y=Asin(ωx+φ)(A<0,ω>0,|φ|≤ ![]() )图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
)图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( ) 
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
D.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com