
【题目】三棱锥A﹣BCD的两条棱AB=CD=6,其余各棱长均为5,求三棱锥的内切球半径. 
【答案】解:法一:易知内切球球心O到各面的距离相等.
设E、F为CD、AB的中点,则O在EF上且O为EF的中点.
在△ABE中,AB=6,AE=BE=4,OH= ![]() .
.
解法二:设球心O到各面的距离为R.
4× ![]() S△BCD×R=VA﹣BCD,
S△BCD×R=VA﹣BCD,
∵S△BCD= ![]() ×6×4=12,
×6×4=12,
VA﹣BCD=2VC﹣ABE=6 ![]() .
.
∴4× ![]() ×12R=6
×12R=6 ![]() .
.
∴R= ![]() .
.
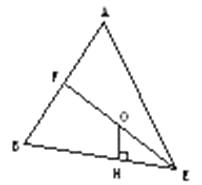
【解析】法一:内切球球心O到各面的距离相等,如图,可以推断出球心在AB和CD的中点的连线的中点,求出OH即可.
法二:先求四面体的体积,再求表面积,利用体积等于表面积和高乘积的 ![]() ,求出内切球半径.
,求出内切球半径.
【考点精析】本题主要考查了棱锥的结构特征的相关知识点,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}满足:a7=a6+2a5 , 若存在两项am , an , 使得 ![]() =4a1 , 则
=4a1 , 则 ![]() +
+ ![]() 的最小值为( )
的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设点M(x0 , y0)是椭圆C: ![]() +y2=1上一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1 , k2
+y2=1上一点,从原点O向圆M:(x﹣x0)2+(y﹣y0)2=r2作两条切线分别与椭圆C交于点P,Q.直线OP,OQ的斜率分别记为k1 , k2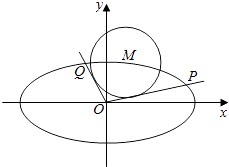
(1)若圆M与x轴相切于椭圆C的右焦点,求圆M的方程;
(2)若r= ![]() ,①求证:k1k2=﹣
,①求证:k1k2=﹣ ![]() ;②求OPOQ的最大值.
;②求OPOQ的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1 , k2 , 且k1+k2=8,证明:直线AB过定点( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为 ![]() (θ为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系.
(θ为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系.
(1)写出曲线C的极坐标方程;
(2)设点M的极坐标为( ![]() ),过点M的直线l与曲线C相交于A,B两点,若|MA|=2|MB|,求AB的弦长.
),过点M的直线l与曲线C相交于A,B两点,若|MA|=2|MB|,求AB的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职业学校的王亮同学到一家贸易公司实习,恰逢该公司要通过海运出口一批货物,王亮同学随公司负责人到保险公司洽谈货物运输期间的投保事宜,保险公司提供了缴纳保险费的两种方案:
①一次性缴纳50万元,可享受9折优惠;
②按照航行天数交纳:第一天缴纳0.5元,从第二天起每天交纳的金额都是其前一天的2倍,共需交纳20天.
请通过计算,帮助王亮同学判断那种方案交纳的保费较低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com