已知复数z=3+ai,且|z-2|<2,求实数a的取值范围.
【答案】
分析:解法一:利用模的定义,从两个已知条件中消去z,再由得数的模的公式转化为转化a的不等式,解出a的取值范围;
解法二:利用复数的几何意义,由条件|z-2|<2可知,z在复平面内对应的点z在以(2,0)为圆心,2为半径的圆内(不包括边界),由z=3+ai可知z对应的点Z在直线x=3上,由得数的几何意义得出复数z=3+ai对应的点的轨迹,由图形得出参数a的取值范围
解答: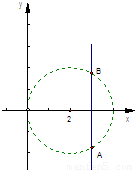
解:解法一:
利用模的定义,从两个已知条件中消去z.
∵z=3+ai(a∈R),由|z-2|<2,得|3+ai-2|<2,即|1+ai|<2,
解得
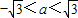
.
解法二:
利用复数的几何意义,由条件|z-2|<2可知,z在复平面内对应的点z在以(2,0)为圆心,2为半径的圆内(不包括边界),由z=3+ai可知z对应的点Z在直线x=3上,所以线段AB(除去端点)为动点Z的集合.由图可知
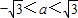
.
点评:本题考查复数的代数表示法及其几何意义,解题的关键是理解复数的代数形式及其几何意义,将问题转化不等式求解或将问题转化为图象利用几何关系求解,本题考查了转化的思想,数形结合的思想,是复数中较为典型的题,

 解:解法一:
解:解法一: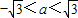 .
.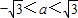 .
.

 优百分课时互动系列答案
优百分课时互动系列答案