
”¾ĢāÄæ”æĶĻŃÓÖ¢×ÜŹĒ±ķĻÖŌŚø÷ÖÖŠ”ŹĀÉĻ£¬µ«ČÕ»żŌĀĄŪ£¬ĢŲ±šÓ°ĻģøöČĖ·¢Õ¹£®Ä³Š£µÄŅ»øöÉē»įŹµ¼łµ÷²éŠ”×飬ŌŚ¶ŌøĆŠ£Ń§Éś½ųŠŠ”°ŹĒ·ńÓŠĆ÷ĻŌĶĻŃÓÖ¢”±µÄµ÷²éÖŠ£¬Ė껜·¢·ÅĮĖ110·ŻĪŹ¾ķ£®¶ŌŹÕ»ŲµÄ100·ŻÓŠŠ§ĪŹ¾ķ½ųŠŠĶ³¼Ę£¬µĆµ½ČēĻĀ![]() ĮŠĮŖ±ķ£ŗ
ĮŠĮŖ±ķ£ŗ
ÓŠĆ÷ĻŌĶĻŃÓÖ¢ | ĪŽĆ÷ĻŌĶĻŃÓÖ¢ | ŗĻ¼Ę | |
ÄŠ | 35 | 25 | 60 |
Å® | 30 | 10 | 40 |
ŗĻ¼Ę | 65 | 35 | 100 |
£Ø¢ń£©°“Å®ÉśŹĒ·ńÓŠĆ÷ĻŌĶĻŃÓÖ¢½ųŠŠ·Ö²ć£¬ŅŃ¾“Ó40·ŻÅ®ÉśĪŹ¾ķÖŠ³éČ”ĮĖ8·ŻĪŹ¾ķ£¬ĻÖ“ÓÕā8·ŻĪŹ¾ķÖŠŌŁĖ껜³éČ”3·Ż£¬²¢¼ĒĘäÖŠĪŽĆ÷ĻŌĶĻŃÓÖ¢µÄĪŹ¾ķµÄ·ŻŹżĪŖ![]() £¬ŹŌĒóĖ껜±äĮæ
£¬ŹŌĒóĖ껜±äĮæ![]() µÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū£»
µÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū£»
£Ø¢ņ£©ČōŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż![]() µÄĒ°ĢįĻĀČĻĪŖĪŽĆ÷ĻŌĶĻŃÓÖ¢ÓėŠŌ±šÓŠ¹Ų£¬ÄĒĆ“øł¾ŻĮŁ½ēÖµ±ķ£¬×ī¾«Č·µÄ
µÄĒ°ĢįĻĀČĻĪŖĪŽĆ÷ĻŌĶĻŃÓÖ¢ÓėŠŌ±šÓŠ¹Ų£¬ÄĒĆ“øł¾ŻĮŁ½ēÖµ±ķ£¬×ī¾«Č·µÄ![]() µÄÖµÓ¦ĪŖ¶ąÉŁ£æĒėĖµĆ÷ĄķÓÉ£®
µÄÖµÓ¦ĪŖ¶ąÉŁ£æĒėĖµĆ÷ĄķÓÉ£®
ø½£ŗ¶ĄĮ¢ŠŌ¼ģŃéĶ³¼ĘĮæ £¬ĘäÖŠ
£¬ĘäÖŠ![]() £®
£®
¶ĄĮ¢ŠŌ¼ģŃéĮŁ½ēÖµ±ķ£ŗ
| 0£®25 | 0£®15 | 0£®10 | 0£®05 | 0£®025 |
| 1£®323 | 2£®072 | 2£®706 | 3£®841 | 5£®024 |
”¾“š°ø”æ£Ø¢ń£©
![]() µÄ·Ö²¼ĮŠĪŖ£ŗ
µÄ·Ö²¼ĮŠĪŖ£ŗ
| 0 | 1 | 2 |
|
|
|
|
![]() ;
;
£Ø¢ņ£©![]() £®
£®
”¾½āĪö”æŹŌĢā·ÖĪö:£Ø¢ń£©·Ö²ć“Ó ”°ĪŽÓŠĆ÷ĻŌĶĻŃÓÖ¢”±Ąļ³é![]() ČĖ£®ĪŽĆ÷ĻŌĶĻŃÓÖ¢µÄĪŹ¾ķµÄ·ŻŹżĪŖ
ČĖ£®ĪŽĆ÷ĻŌĶĻŃÓÖ¢µÄĪŹ¾ķµÄ·ŻŹżĪŖ![]() £¬Ė껜±äĮæX=0£¬1£¬2£®ĄūÓĆ”°³¬¼øŗĪ·Ö²¼”±¼“æÉµĆ³ö·Ö²¼ĮŠ¼°Ę䏿ѧʌĶū£»
£¬Ė껜±äĮæX=0£¬1£¬2£®ĄūÓĆ”°³¬¼øŗĪ·Ö²¼”±¼“æÉµĆ³ö·Ö²¼ĮŠ¼°Ę䏿ѧʌĶū£»
£Ø¢ņ£©øł¾Ż”°¶ĄĮ¢ŠŌ¼ģŃéµÄ»ł±¾Ė¼ĻėµÄÓ¦ÓĆ”±¼ĘĖć¹«Ź½æɵĆ![]() µÄ¹Ū²āÖµ
µÄ¹Ū²āÖµ![]() £¬¼“æÉµĆ³ö£®
£¬¼“æÉµĆ³ö£®
ŹŌĢā½āĪö:£Ø¢ń£©Å®ÉśÖŠ“Ó”°ÓŠĆ÷ĻŌĶĻŃÓÖ¢”±Ąļ³é![]() ČĖ£¬”°ĪŽÓŠĆ÷ĻŌĶĻŃÓÖ¢”±Ąļ³é
ČĖ£¬”°ĪŽÓŠĆ÷ĻŌĶĻŃÓÖ¢”±Ąļ³é![]() ČĖ£®
ČĖ£®
ŌņĖ껜±äĮæ![]() £¬
£¬
”ą![]() £¬
£¬ ![]() £¬
£¬ ![]() £®
£®
![]() µÄ·Ö²¼ĮŠĪŖ£ŗ
µÄ·Ö²¼ĮŠĪŖ£ŗ
| 0 | 1 | 2 |
|
|
|
|
![]() £®
£®
£Ø¢ņ£©ÓÉĢāÉčĢõ¼žµĆ![]() £¬
£¬
ÓÉĮŁ½ēÖµ±ķæÉÖŖ£ŗ ![]() £¬”ą
£¬”ą![]() £®
£®
µćĒē£ŗ±¾Ģāæ¼²éµÄŹĒ³¬¼øŗĪ·Ö²¼ŗĶ¶ĄĮ¢ŠŌ¼ģŃéĪŹĢā.£Ø¢ń£©ŅŖ×¢ŅāĒų·ÖŹĒ³¬¼øŗĪ·Ö²¼»¹ŹĒ¶žĻī·Ö²¼£¬·Ö²ć“Ó ”°ĪŽÓŠĆ÷ĻŌĶĻŃÓÖ¢”±Ąļ³é![]() ČĖ£®ĪŽĆ÷ĻŌĶĻŃÓÖ¢µÄĪŹ¾ķµÄ·ŻŹżĪŖ
ČĖ£®ĪŽĆ÷ĻŌĶĻŃÓÖ¢µÄĪŹ¾ķµÄ·ŻŹżĪŖ![]() =0£¬1£¬2£®ĄūÓĆ”°³¬¼øŗĪ·Ö²¼”±¼“æÉµĆ³ö·Ö²¼ĮŠ¼°Ę䏿ѧʌĶū£»£Ø¢ņ£©øł¾Ż”°¶ĄĮ¢ŠŌ¼ģŃéµÄ»ł±¾Ė¼ĻėµÄÓ¦ÓĆ”±¼ĘĖć¹«Ź½æɵĆ
=0£¬1£¬2£®ĄūÓĆ”°³¬¼øŗĪ·Ö²¼”±¼“æÉµĆ³ö·Ö²¼ĮŠ¼°Ę䏿ѧʌĶū£»£Ø¢ņ£©øł¾Ż”°¶ĄĮ¢ŠŌ¼ģŃéµÄ»ł±¾Ė¼ĻėµÄÓ¦ÓĆ”±¼ĘĖć¹«Ź½æɵĆ![]() µÄ¹Ū²āÖµ
µÄ¹Ū²āÖµ![]() £¬¼“æÉµĆ³ö£®
£¬¼“æÉµĆ³ö£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹżf£Øx£©=2sin£Ø¦Ųx+¦Õ£©£Ø¦Ų£¾0£¬© ![]() £¼¦Õ£¼
£¼¦Õ£¼ ![]() £©µÄ²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£»
£©µÄ²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£» 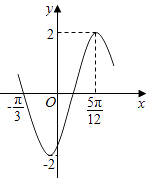
£Ø1£©Ēó¦Ų£¬¦Õ£»
£Ø2£©½«y=f£Øx£©µÄĶ¼ĻóĻņ×óĘ½ŅĘ¦Č£Ø¦Č£¾0£©øöµ„Ī»³¤¶Č£¬µĆµ½y=g£Øx£©µÄĶ¼Ļó£¬Čōy=g£Øx£©Ķ¼ĻóµÄŅ»øö¶Ō³ĘµćĪŖ£Ø ![]() £¬0£©£¬Ēó¦ČµÄ×īŠ”Öµ£®
£¬0£©£¬Ēó¦ČµÄ×īŠ”Öµ£®
£Ø3£©¶ŌČĪŅāµÄx”Ź[ ![]() £¬
£¬ ![]() ]Ź±£¬·½³Ģf£Øx£©=mÓŠĮ½øö²»µČøł£¬ĒómµÄȔֵ·¶Ī§£®
]Ź±£¬·½³Ģf£Øx£©=mÓŠĮ½øö²»µČøł£¬ĒómµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŌŚ³¤·½ĢåABCD©A1B1C1D1ÖŠ£¬BC=2AB=4£¬ ![]() £¬EŹĒA1D1µÄÖŠµć£®
£¬EŹĒA1D1µÄÖŠµć£®
£Ø¢ń£©ŌŚĘ½ĆęA1B1C1D1ÄŚ£¬Ēė×÷³ö¹żµćEÓėCE“¹Ö±µÄÖ±Ļßl£¬²¢Ö¤Ć÷l”ĶCE£»
£Ø¢ņ£©Éč£Ø¢ń£©ÖŠĖł×÷Ö±ĻßlÓėCEČ·¶ØµÄĘ½ĆęĪŖ¦Į£¬ĒóµćC1µ½Ę½Ćę¦ĮµÄ¾ąĄė£®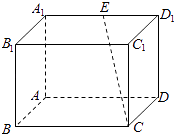
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōŗÆŹż![]() ¶Ō¶ØŅåÓņÄŚµÄČĪŅā
¶Ō¶ØŅåÓņÄŚµÄČĪŅā![]() £¬µ±
£¬µ±![]() Ź±£¬×ÜÓŠ
Ź±£¬×ÜÓŠ![]() £¬Ōņ³ĘŗÆŹż
£¬Ōņ³ĘŗÆŹż![]() ĪŖµ„µ÷ŗÆŹż£¬ĄżČēŗÆŹż
ĪŖµ„µ÷ŗÆŹż£¬ĄżČēŗÆŹż![]() ŹĒµ„“æŗÆŹż£¬µ«ŗÆŹż
ŹĒµ„“æŗÆŹż£¬µ«ŗÆŹż![]() ²»ŹĒµ„“æŗÆŹż£¬ĻĀĮŠĆüĢā£ŗ
²»ŹĒµ„“æŗÆŹż£¬ĻĀĮŠĆüĢā£ŗ
¢ŁŗÆŹż![]() ŹĒµ„“æŗÆŹż£»
ŹĒµ„“æŗÆŹż£»
¢Śµ±![]() Ź±£¬ŗÆŹż
Ź±£¬ŗÆŹż![]() ŌŚ
ŌŚ![]() ŹĒµ„“æŗÆŹż£»
ŹĒµ„“æŗÆŹż£»
¢ŪČōŗÆŹż![]() ĪŖĘä¶ØŅåÓņÄŚµÄµ„“æŗÆŹż£¬
ĪŖĘä¶ØŅåÓņÄŚµÄµ„“æŗÆŹż£¬ ![]() £¬Ōņ
£¬Ōņ![]()
¢ÜČōŗÆŹż![]() ŹĒµ„“æŗÆŹżĒŅŌŚĘä¶ØŅåÓņÄŚæɵ¼£¬ŌņŌŚĘä¶ØŅåÓņÄŚŅ»¶Ø“ęŌŚ
ŹĒµ„“æŗÆŹżĒŅŌŚĘä¶ØŅåÓņÄŚæɵ¼£¬ŌņŌŚĘä¶ØŅåÓņÄŚŅ»¶Ø“ęŌŚ![]() Ź¹Ęäµ¼Źż
Ź¹Ęäµ¼Źż![]() £¬ĘäÖŠÕżČ·µÄĆüĢāĪŖ__________£®£ØĢīÉĻĖłÓŠÕżČ·µÄĆüĢāŠņŗÅ£©
£¬ĘäÖŠÕżČ·µÄĆüĢāĪŖ__________£®£ØĢīÉĻĖłÓŠÕżČ·µÄĆüĢāŠņŗÅ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉčŗÆŹżg£Øx£©=x2©2£¬f£Øx£©= ![]() £¬Ōņf£Øx£©µÄÖµÓņŹĒ£Ø £©
£¬Ōņf£Øx£©µÄÖµÓņŹĒ£Ø £©
A.![]()
B.[0£¬+”Ž£©??
C.![]()
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¼ÆŗĻA={x|log2 ![]() ”Ü1}£¬B={x|x2©2x+1©k2”Ż0}£®
”Ü1}£¬B={x|x2©2x+1©k2”Ż0}£®
£Ø1£©Ēó¼ÆŗĻA£»
£Ø2£©ČōA”ÉB”Ł£¬Ē󏵏żkµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ³¤·½ŠĪABCDÖŠ£¬AB=2£¬AD=1£¬MĪŖDCµÄÖŠµć£®½«”÷ADMŃŲAMÕŪĘš£¬Ź¹µĆĘ½ĆęADM”ĶĘ½ĆęABCM£¬EĪŖBDµÄÖŠµć£® 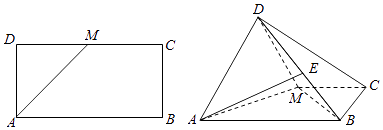
£Ø1£©ĒóÖ¤£ŗBM”ĶĘ½ĆęADM£»
£Ø2£©ĒóÖ±ĻßAEÓėĘ½ĆęADMĖł³É½ĒµÄÕżĻŅÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ“ÓÄ³Ń§Š£øßȿ𼶹²800ĆūÄŠÉśÖŠĖ껜³éČ”50Ćū²āĮæÉķøߣ¬¾Ż²āĮæ±»²āѧɜÉķøßČ«²æ½éÓŚ155cmŗĶ195cmÖ®¼ä£¬½«²āĮæ½į¹ū°“ČēĻĀ·½Ź½·Ö³É°Ė×é£ŗµŚŅ»×é[155£¬160£©”¢µŚ¶ž×é[160£¬165£©£»”µŚ°Ė×é[190£¬195]£¬ČēĶ¼ŹĒ°“ÉĻŹö·Ö×é·½·ØµĆµ½µÄʵĀŹ·Ö²¼Ö±·½Ķ¼µÄŅ»²æ·Ö£¬ŅŃÖŖµŚĮł×é±ČµŚĘß×鶹1ČĖ£¬µŚŅ»×éŗĶµŚ°Ė×éČĖŹżĻąĶ¬£®
£ØI£©ĒóµŚĮł×锢µŚĘß×éµÄʵĀŹ²¢²¹³äĶźÕūʵĀŹ·Ö²¼Ö±·½Ķ¼£»
£Ø¢ņ£©Čō“ÓÉķøߏōÓŚµŚĮł×éŗĶµŚ°Ė×éµÄĖłÓŠÄŠÉśÖŠĖ껜³éČ”Į½ĆūÄŠÉś£¬¼ĒĖūĆĒµÄÉķøß·Ö±šĪŖx”¢y£¬ĒóĀś×ć|x©y|”Ü5µÄŹĀ¼žøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
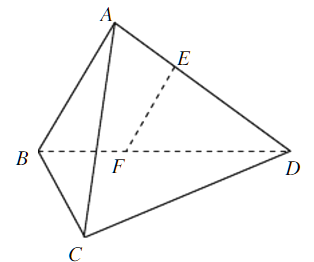
”¾ĢāÄæ”æČēĶ¼£¬ŌŚČżĄā׶A-BCDÖŠ£¬AB”ĶAD£¬BC”ĶBD£¬Ę½ĆęABD”ĶĘ½ĆęBCD£¬µćE”¢F£ØEÓėA”¢D²»ÖŲŗĻ£©·Ö±šŌŚĄāAD£¬BDÉĻ£¬ĒŅEF”ĶAD.
ĒóÖ¤£ŗ£Ø1£©EF”ĪĘ½ĆęABC£»
£Ø2£©AD”ĶAC.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com