
【题目】王明参加某卫视的闯关活动,该活动共3关.设他通过第一关的概率为0.8,通过第二、第三关的概率分别为p,q,其中![]() ,并且是否通过不同关卡相互独立.记ξ为他通过的关卡数,其分布列为:
,并且是否通过不同关卡相互独立.记ξ为他通过的关卡数,其分布列为:
ξ | 0 | 1 | 2 | 3 |
P | 0.048 | a | b | 0.192 |
(Ⅰ)求王明至少通过1个关卡的概率;
(Ⅱ)求p,q的值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
, ![]() 为原点,
为原点, ![]() ,
, ![]() 是
是![]() 轴上的两个动点,且
轴上的两个动点,且![]() ,直线
,直线![]() 和
和![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
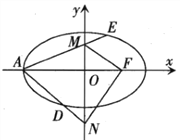
(Ⅰ)求![]() 的面积的最小值;
的面积的最小值;
(Ⅱ)证明: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)=(x﹣l)(log3a)2﹣6(log3a)x+x+l在x∈[0,l]内恒为正值,则a的取值范围是( )
A.﹣1<a< ![]()
B.a< ![]()
C.a> ![]()
D.![]() <a<
<a< ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月13日第30届大连国际马拉松赛举行,某单位的10名跑友报名参加了半程马拉松、10公里健身跑、迷你马拉松3个项目(每人只报一项),报名情况如下:
项目 | 半程马拉松 | 10公里健身跑 | 迷你马拉松 |
人数 | 2 | 3 | 5 |
(其中:半程马拉松![]() 公里,迷你马拉松
公里,迷你马拉松![]() 公里)
公里)
(1)从10人中选出2人,求选出的两人赛程距离之差大于10公里的概率;
(2)从10人中选出2人,设![]() 为选出的两人赛程距离之和,求随机变量
为选出的两人赛程距离之和,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]()
(1)求函数f(x)的解析式;
(2)若方程3[f(x)]2﹣f(x)+m=0在x∈( ![]() ,
, ![]() )内有两个不同的解,求实数m的取值范围.
)内有两个不同的解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分别求出适合下列条件的直线方程:
(Ⅰ)经过点![]() 且在x轴上的截距等于在y轴上截距的2倍;
且在x轴上的截距等于在y轴上截距的2倍;
(Ⅱ)经过直线2x+7y﹣4=0与7x﹣21y﹣1=0的交点,且和A(﹣3,1),B(5,7)等距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
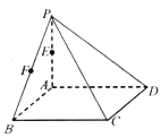
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() 的中点.
的中点.
(1)在图中画出过点![]() 的平面
的平面![]() ,使得
,使得![]() 平面
平面![]() (须说明画法,并给予证明);
(须说明画法,并给予证明);
(2)若过点![]() 的平面
的平面![]() 平面
平面![]() 且截四棱锥
且截四棱锥![]() 所得截面的面积为
所得截面的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com