
解法一:设二次函数解析式为y=ax2+bx+c,
依题意有x=-![]() =-
=-![]() . ①
. ①
图象过点(0,-1),则有c=-1. ②
又截轴的弦长为4,设ax2+bx+c=0的两根为x1、x2,由韦达定理有
|x1-x2|=![]() =4. ③
=4. ③
由①②③式联立解得a=![]() ,b=
,b=![]() ,c=-1.
,c=-1.
∴二次函数解析式为
y=![]() x2+
x2+![]() x-1.
x-1.
解法二:设y=a(x+![]() )2+m,由条件得
)2+m,由条件得
-1=2a+m. ①
弦长为4,令y=0,(x+![]() )2=-
)2=-![]() ,
,
则有x=-![]() ±
±![]() .
.
由|x1-x2|=4,
∴2![]() =4. ②
=4. ②
联立①②式解得a=![]() ,m=-2.
,m=-2.
∴二次函数解析式为
y=![]() (x+
(x+![]() )2-2.
)2-2.
解法三:∵对称轴为x=-![]() ,又截x轴的弦长为4,则图象与x轴的交点为x1=-2-
,又截x轴的弦长为4,则图象与x轴的交点为x1=-2-![]() ,x2=2-
,x2=2-![]() .
.
设二次函数为y=a(x+2+![]() )(x-2+
)(x-2+![]() ),
),
又(0,-1)在图象上,则有-1=a(2+![]() )(-2+
)(-2+![]() ).
).
∴a=![]() ,二次函数解析式为y=
,二次函数解析式为y=![]() x2+
x2+![]() x-1.
x-1.


科目:高中数学 来源:高考数学一轮复习必备(第14课时):第二章 函数-二次函数(解析版) 题型:解答题
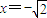 ,截x轴上的弦长为4,且过点(0,-1),求函数的解析式.
,截x轴上的弦长为4,且过点(0,-1),求函数的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com