
【题目】设椭圆C: ![]() =1(a>b>0)的焦点F1 , F2 , 过右焦点F2的直线l与C相交于P、Q两点,若△PQF1的周长为短轴长的2
=1(a>b>0)的焦点F1 , F2 , 过右焦点F2的直线l与C相交于P、Q两点,若△PQF1的周长为短轴长的2 ![]() 倍.
倍.
(Ⅰ)求C的离心率;
(Ⅱ)设l的斜率为1,在C上是否存在一点M,使得 ![]() ?若存在,求出点M的坐标;若不存在,说明理由.
?若存在,求出点M的坐标;若不存在,说明理由.
【答案】解:(Ⅰ)∵椭圆C: ![]() =1(a>b>0)的焦点F1,F2,过右焦点F2的直线l与C相交于P、Q两点,
=1(a>b>0)的焦点F1,F2,过右焦点F2的直线l与C相交于P、Q两点,
△PQF1的周长为短轴长的2 ![]() 倍,△PQF1的周长为4a
倍,△PQF1的周长为4a
∴依题意知 ![]() ,即
,即 ![]()
∴C的离心率 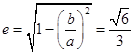
(Ⅱ)设椭圆方程为 ![]() ,直线的方程为y=x﹣c,
,直线的方程为y=x﹣c,
代入椭圆方程得 ![]()
设P(x1,y1),Q(x2,y2),则 ![]() ,
, ![]()
设M(x0,y0),则 ![]() ①
①
由 ![]() 得
得 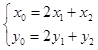
代入①得 ![]()
因为 ![]() ,
, ![]() ,
,
所以 ![]() ②
②
而 ![]()
从而②式不成立.
故不存在点M,使 ![]() 成立
成立
【解析】(Ⅰ)由椭圆的焦点F1,F2,过右焦点F2的直线l与C相交于P、Q两点,△PQF1的周长为短轴长的2 ![]() 倍,得到
倍,得到 ![]() ,由此能求出椭圆C的离心率.(Ⅱ)设椭圆方程为
,由此能求出椭圆C的离心率.(Ⅱ)设椭圆方程为 ![]() ,直线的方程为y=x﹣c,代入椭圆方程得
,直线的方程为y=x﹣c,代入椭圆方程得 ![]() ,由此利用韦达定理、椭圆性质、向量知识,结合已知条件能求出不存在点M,使
,由此利用韦达定理、椭圆性质、向量知识,结合已知条件能求出不存在点M,使 ![]() 成立.
成立.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣2ax(其中a∈R).
(Ⅰ)当a=1时,求函数f(x)的图象在x=1处的切线方程;
(Ⅱ)若f(x)≤1恒成立,求a的取值范围;
(Ⅲ)设g(x)=f(x)+ ![]() x2 , 且函数g(x)有极大值点x0 , 求证:x0f(x0)+1+ax02>0.
x2 , 且函数g(x)有极大值点x0 , 求证:x0f(x0)+1+ax02>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,面ABB1A1为矩形,AB=1,AA1= ![]() ,D为AA1的中点,BD与AB1交于点O,CO⊥面ABB1A1
,D为AA1的中点,BD与AB1交于点O,CO⊥面ABB1A1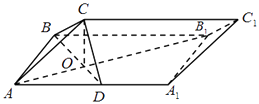
(Ⅰ)证明:BC⊥AB1
(Ⅱ)若OC=OA,求二面角A﹣BC﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线x2﹣ ![]() =1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
=1的右支上一点P,分别向圆C1:(x+4)2+y2=4和圆C2:(x﹣4)2+y2=1作切线,切点分别为M,N,则|PM|2﹣|PN|2的最小值为( )
A.10
B.13
C.16
D.19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列两个命题: 命题p::若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为 ![]() .命题q:设
.命题q:设 ![]() ,
, ![]() 是两个非零向量,则“
是两个非零向量,则“ ![]() =|
=| ![]() |”是“
|”是“ ![]() 与
与 ![]() 共线”的充分不必要条件,那么,下列命题中为真命题的是( )
共线”的充分不必要条件,那么,下列命题中为真命题的是( )
A.p∧q
B.¬p
C.p∧(¬q)
D.(¬p)∨(q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前项和为Sn , 且 ![]() ,用[x]表示不超过x的最大整数,如[﹣0.1]=﹣1,[1.6]=1,设bn=[an],则数列{bn}的前2n项和b1+b2+b3+b4++b2n﹣1+b2n= .
,用[x]表示不超过x的最大整数,如[﹣0.1]=﹣1,[1.6]=1,设bn=[an],则数列{bn}的前2n项和b1+b2+b3+b4++b2n﹣1+b2n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若
=1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若 ![]() =λ
=λ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |+|
|+| ![]() |=8,则双曲线的标准方程为( )
|=8,则双曲线的标准方程为( )
A.x2﹣ ![]() =1
=1
B.![]() ﹣y2=1
﹣y2=1
C.![]() =1
=1
D.x2﹣ ![]() =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com