
【题目】在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C1的极坐标方程为ρ=4cosθ,直线C2的参数方程为![]() (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程和直线C2的普通方程;
(2)若P(1,0),直线C2与曲线C1相交于A,B两点,求|PA||PB|的值.
【答案】(1)曲线C1:x2+y2﹣4x=0;直线C2:xsinα﹣ycosα﹣sinα=0(2)3
【解析】
(1)求曲线C1的直角坐标方程需利用直角坐标与极坐标关系互化关系式x=ρcosθ,y=ρsinθ,x2+y2=ρ2,将ρ=4cosθ,等式两边乘ρ得ρ2=4ρcosθ代入即可,直线C2的参数方程消去参数t即为普通方程;
(2)因为P(1,0)在直线C2上,将直线C2的参数方程![]() (t为参数)代入曲线C1:x2+y2﹣4x=0,设A,B对应的参数分别为t1,t2,根据根与系数关系可得则t1t2=﹣3,故可求|PA||PB|=|t1t2|=3.
(t为参数)代入曲线C1:x2+y2﹣4x=0,设A,B对应的参数分别为t1,t2,根据根与系数关系可得则t1t2=﹣3,故可求|PA||PB|=|t1t2|=3.
(1)曲线C1的极坐标方程为ρ=4cosθ,由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,
可得ρ2=4ρcosθ,即为x2+y2﹣4x=0,
直线C2的参数方程为![]() (t为参数),
(t为参数),
可得xsinα﹣ycosα﹣sinα=0;
(2)因为P(1,0)在直线C2上,
将直线C2的参数方程![]() (t为参数)代入x2+y2﹣4x=0,
(t为参数)代入x2+y2﹣4x=0,
可得(1+tcosα)2+(tsinα)2﹣4(1+tcosα)=0,
化为t2﹣2tcosα﹣3=0,
设A,B对应的参数分别为t1,t2,则t1t2=﹣3,
可得|PA||PB|=|t1t2|=3.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收入
收入![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用……等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.
专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用……等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.
新个税政策的税率表部分内容如下:
级数 | 一级 | 二级 | 三级 | 四级 | … |
每月应纳税所得额(含税) | 不超过3000元的部分 | 超过3000元至12000元的部分 | 超过12000元至25000元的部分 | 超过25000元至35000元的部分 | … |
税率(%) | 3 | 10 | 20 | 25 | … |
(1)现有李某月收入19600元,膝下有一名子女,需要赡养老人,(除此之外,无其它专项附加扣除)请问李某月应缴纳的个税金额为多少?
(2)现收集了某城市50名年龄在40岁到50岁之间的公司白领的相关资料,通过整理资料可知,有一个孩子的有40人,没有孩子的有10人,有一个孩子的人中有30人需要赡养老人,没有孩子的人中有5人需要赡养老人,并且他们均不符合其它专项扣除(受统计的50人中,任何两人均不在一个家庭).若他们的月收入均为20000元,试求在新个税政策下这50名公司白领的月平均缴纳个税金额为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆![]() 极坐标方程为
极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求直线
时,求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与圆
与圆![]() 的交点为
的交点为![]() 、
、![]() ,证明:
,证明:![]() 是与
是与![]() 无关的定值.
无关的定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinxcosx![]() cos2x+1
cos2x+1
(1)求f(x)的最小正周期和最大值,并写出取得最大值时x的集合;
(2)将f(x)的函数图象向左平移φ(φ>0)个单位后得到的函数g(x)是偶函数,求φ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果无穷数列{an}满足条件:①![]() ;② 存在实数M,使得an≤M,其中n∈N*,那么我们称数列{an}为Ω数列.
;② 存在实数M,使得an≤M,其中n∈N*,那么我们称数列{an}为Ω数列.
(1)设数列{bn}的通项为bn=20n-2n,且是Ω数列,求M的取值范围;
(2)设{cn}是各项为正数的等比数列,Sn是其前n项和,c3=![]() ,S3=
,S3=![]() ,证明:数列{Sn}是Ω数列;
,证明:数列{Sn}是Ω数列;
(3)设数列{dn}是各项均为正整数的Ω数列,求证:dn≤dn+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,己知圆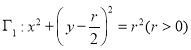 和双曲线
和双曲线![]() ,记
,记![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴负半轴的公共点分别为
轴负半轴的公共点分别为![]() 、
、![]() ,又记
,又记![]() 与
与![]() 在第一、第四象限的公共点分别为
在第一、第四象限的公共点分别为![]() 、
、![]() .
.

(1)若![]() ,且
,且![]() 恰为
恰为![]() 的左焦点,求
的左焦点,求![]() 的两条渐近线的方程;
的两条渐近线的方程;
(2)若![]() ,且
,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)若![]() 恰为
恰为![]() 的左焦点,求证:在
的左焦点,求证:在![]() 轴上不存在这样的点
轴上不存在这样的点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
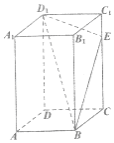
【题目】如图,已知在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 上的一个动点,平面
上的一个动点,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,给出下列命题:
,给出下列命题:
①四棱锥![]() 的体积为20;
的体积为20;
②存在唯一的点![]() ,使截面四边形
,使截面四边形![]() 的周长取得最小值
的周长取得最小值![]() ;
;
③当![]() 点不与
点不与![]() ,
,![]() 重合时,在棱
重合时,在棱![]() 上均存在点
上均存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④存在唯一的点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.
其中正确的命题是_____(填写所有正确的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com