
【题目】已知关于x的不等式![]() 的解集为
的解集为![]() .
.
(1)求a,b的值.
(2)当![]() 时,解关于x的不等式
时,解关于x的不等式![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
试题
(1)利用韦达定理可得![]() ;
;
(2)结合(1)的结论分类讨论实数c的范围即可求得不等式的解集.
试题解析:
解:(1)因为不等式ax2-3x+2>0的解集为{x|x<1或x>b}
所以x1=1与x2=b是方程ax2-3x+2=0的两个实数根
b>1且a>0
得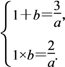 解得
解得![]()
(2)不等式ax2-(ac+b)x+bc<0,
即x2-(2+c)x+2c<0,即(x-2)(x-c)<0.
当c>2时,不等式(x-2)(x-c)<0的解集为{x|2<x<c};
当c<2时,不等式(x-2)(x-c)<0的解集为{x|c<x<2};
当c=2时,不等式(x-2)(x-c)<0的解集为


科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”,若
的“不动点”,若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”,函数
的“稳定点”,函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() ,那么,
,那么,
(1)求函数![]() 的“稳定点”;
的“稳定点”;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且c= ![]() asinC﹣ccosA
asinC﹣ccosA
(1)求A;
(2)若a=2,△ABC的面积为 ![]() ,求b,c.
,求b,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有( )
①函数y=![]() 的定义域为{x|x≥1};
的定义域为{x|x≥1};
②函数y=x2+x+1在(0,+∞)上是增函数;
③函数f(x)=x3+1(x∈R),若f(a)=2,则f(-a)=-2;
④已知f(x)是R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com