
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为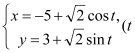 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 两点的极坐标和
两点的极坐标和![]() 面积的最小值.
面积的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
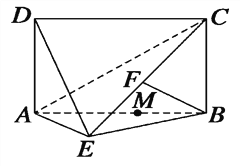
【题目】如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,
BF⊥平面ACE,且点F在CE上.
(1)求证:AE⊥BE;
(2)求三棱锥D—AEC的体积;
(3)设点M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,
使得MN∥平面DAE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 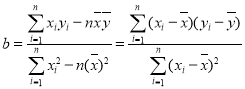 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 为原点的直角坐标系中,点
为原点的直角坐标系中,点![]() 为
为![]() 的直角顶点,已知
的直角顶点,已知![]() ,且点
,且点![]() 的纵坐标大于0.
的纵坐标大于0.
(1)求![]() 的坐标;
的坐标;
(2)求圆![]() 关于直线
关于直线![]() 对称的圆
对称的圆![]() 的方程;在直线
的方程;在直线![]() 上是否存在点
上是否存在点![]() ,过点
,过点![]() 的任意一条直线如果和圆
的任意一条直线如果和圆![]() 圆
圆![]() 都相交,则该直线被两圆截得的线段长相等,如果存在求出点
都相交,则该直线被两圆截得的线段长相等,如果存在求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,
,![]() 是椭圆上一点, 记直线
是椭圆上一点, 记直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,且有
,且有![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点, 以
两点, 以![]() 、
、![]() 为直径的圆经过原点, 且线段
为直径的圆经过原点, 且线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距为
轴上的截距为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是![]() .
.
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() .( 结果用分数表示)
.( 结果用分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com