
����Ŀ��һ̨����ʹ�õ�ʱ��ϳ�����������ʹ�ã�������ͬ��ת������������ij��е�����һЩ����ȱ�㣬ÿСʱ������ȱ������Ķ��٣��������ת�ٶȶ��仯���±�Ϊ��������Ľ����
ת��x(ת/��) | 16 | 14 | 12 | 8 |
ÿСʱ������ȱ��������y(��) | 11 | 9 | 8 | 5 |
��1������ɢ��ͼ�����ϵ��r�Ĵ�С�жϱ���y��x�Ƿ�������أ�Ϊʲô��
��2�����y��x��������ع�ϵ����ع�ֱ�߷��̣�
��3����ʵ�������У�����ÿСʱ�IJ�Ʒ����ȱ���������Ϊ10������ô��������ת�ٶ�Ӧ������ʲô��Χ�ڣ�
���������ȷ��0.001���ο����ݣ�![]() ��
��![]()
![]() ��
��![]() ��
��
�ع�����йع�ʽ��r= ��
�� ��
��![]() ��
��
���𰸡���1��y��x����������ع�ϵ��2��![]() ��3��
��3��![]()
��������
��1���������������ݸ��ݹ�ʽ����������������ϵ�����õ���ع�ϵ�����ƴ���![]() ,�õ�������������������ع�ϵ����2����������������������ƽ�������������С���˷������Իع鷽�̵�ϵ����ʽ��������������ù�ʽ�ɵ�ϵ��
,�õ�������������������ع�ϵ����2����������������������ƽ�������������С���˷������Իع鷽�̵�ϵ����ʽ��������������ù�ʽ�ɵ�ϵ��![]() ��ֵ���Ӷ����
��ֵ���Ӷ����![]() �������ɵ����Իع鷽������3��������һ�����������Իع鷽�̣�ʹ�ú���ֵС�ڻ����
�������ɵ����Իع鷽������3��������һ�����������Իع鷽�̣�ʹ�ú���ֵС�ڻ����![]() ���������ʽ����.
���������ʽ����.
��1��![]() ��
��![]() ��
��![]()
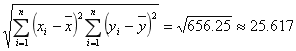
��![]() ��y��x����������ع�ϵ��
��y��x����������ع�ϵ��
��2���⣺![]() ��
��![]() ��
��![]()
��ع�ֱ�߷���Ϊ��![]()
��3��![]() �����
�����![]()


 �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() �ڶ������ϲ���������
�ڶ������ϲ���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() �ֱ���
�ֱ���![]() �ļ���ֵ�ͼ�Сֵ����
�ļ���ֵ�ͼ�Сֵ����![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽��ϡ��°�ʱ�ڵĽ�ͨ�����ij�г�ȡ��12����������ʻ��ʱ�٣��õ���������������λ��km/h��.
�ϰ�ʱ�ڣ�30 33 18 27 32 40 26 28 21 28 35 20
�°�ʱ�ڣ�27 19 32 29 36 29 30 22 25 16 17 30
�þ�Ҷͼ��ʾ��Щ���ݣ����ֱ���Ƴ������ϡ��°�ʱ�ڻ�������ʻ��ƽ��ʱ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ�������ž��õķ�չ���ҹ��������Ӷ���̬�����ı�����2018���������Ի��������������������������Ļ�����رա�һ��ʱ���ڣ������ļ۸�����ϴ�ͬ�ܼ۸�ͬ���������һ�ܡ��ڶ��ܼ����ļ۸�ֱ�Ϊ![]() Ԫ��
Ԫ��![]() Ԫ����λ��kg�����ס������˵Ĺ���ʽ��ͬ����ÿ�ܹ���3kg��������ÿ�ܹ���10ԪǮ����.
Ԫ����λ��kg�����ס������˵Ĺ���ʽ��ͬ����ÿ�ܹ���3kg��������ÿ�ܹ���10ԪǮ����.
������![]() ����ס������ܹ�����ƽ���۸�
����ס������ܹ�����ƽ���۸�
�����жϼס�������˭�Ĺ���ʽ��ʵ�ݣ�ƽ���۸����Ϊʵ�ݣ�����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() �Ƕ�����
�Ƕ�����![]() �ϵĿɵ��������䵼����Ϊ
�ϵĿɵ��������䵼����Ϊ![]() ������
������![]() ����ʽ
����ʽ![]()
![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����绰������ĵ绰���1��ʱ���ӵĸ�����0.1�����2��ʱ���ӵĸ�����0.2�����3��ʱ���ӵĸ�����0.3�����4��ʱ���ӵĸ�����0.35.
��1������ĵ绰����5��֮ǰ���ӵĸ����Ƕ��٣�
��2������ĵ绰��4���������ӵĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f��x����������f��0����1����f��x+1����f��x����2x��
��1������f��x���Ľ���ʽ��
��2��������[��1��1]�ϣ�y��f��x����ͼ�����y��2x+m��ͼ���Ϸ�����ȷ��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() ��,Բ
��,Բ![]() ���������任
���������任![]() ��õ�����
��õ�����![]() ,���ֱ��ֱ��
,���ֱ��ֱ��![]() ������
������![]() ������
������![]() �ཻ��
�ཻ��![]() ����,
����, ![]() ������
������![]() �ཻ��
�ཻ��![]() ����.
����.
(1)������![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
(2)��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P-ABCD�У��ڵ���ABCD�У�AD//BC,AD��CD��Q��AD���е㣬M����PC���е㣬PA=PD=2,BC=![]() AD=1,CD=
AD=1,CD=![]() ,PB=
,PB=![]() ��
��
������֤��ƽ��PAD�͵���ABCD��
������������B-PQM�������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com