
| A. | 212-57 | B. | 211-47 | C. | 210-38 | D. | 29-30 |
分析 先设每个30分钟进去的人数构成数列{an},确定求数列{an}的通项公式,由于从早晨6时30分到上午11时,共有10个30分钟,故需求数列{an}的前10项和,再由等比数列前n项和公式即可得上午11时园内的人数.
解答 解:设每个30分钟进去的人数构成数列{an},则
a1=2=2-0,a2=4-1,a3=8-2,a4=16-3,a5=32-4,…,an=2n-(n-1)
设数列{an}的前n项和为Sn,依题意,
只需求S10=(2-0)+(22-1)+(23-2)+…+(210-9)=(2+22+23+…+210)-(1+2+…+9)=211-47
故选B.
点评 本题考查数列的通项公式,等比数列的前n项和公式,考查将实际问题转化为数学问题,运用数学知识解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | $\frac{1}{84}$ | D. | $\frac{2}{251}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
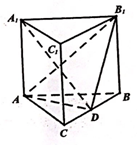 如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为$\frac{π}{3}$,点D线段BC的中点.
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为$\frac{π}{3}$,点D线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3] | B. | [9,+∞) | C. | (-∞,9] | D. | (-∞,9) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l∥α | B. | l⊥α | C. | l?α | D. | A、C都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com