
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,且它的焦距是短轴长的
,且它的焦距是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的方程.
的方程.
(2)若![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点(
上的两个动点(![]() ,
,![]() 两点不关于
两点不关于![]() 轴对称),
轴对称),![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,问是否存在非零常数
,问是否存在非零常数![]() ,使当
,使当![]() 时,
时,![]() 的面积
的面积![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在这样的常数
;(2)存在这样的常数![]() ,此时
,此时![]() .
.
【解析】
(1)将点![]() 的坐标代入椭圆方程,结合
的坐标代入椭圆方程,结合![]() 和
和![]() 列方程组,解方程组求得椭圆的标准方程.(2)设直线
列方程组,解方程组求得椭圆的标准方程.(2)设直线![]() 的方程为
的方程为![]() 和
和![]() 两点的坐标,将
两点的坐标,将![]() 两点两点坐标代入
两点两点坐标代入![]() ,化简得到
,化简得到![]() ①.联立直线
①.联立直线![]() 的方程和椭圆方程,写出韦达定理,利用点到直线距离公式和弦长公式求得三角形
的方程和椭圆方程,写出韦达定理,利用点到直线距离公式和弦长公式求得三角形![]() 的面积的表达式,结合①解得
的面积的表达式,结合①解得![]() 和
和![]() 的值.
的值.
解:(1)因为椭圆![]() :
:![]() 过点
过点![]() ,
,
所以![]() ,
,
又因为该椭圆的焦距是短轴长的![]() 倍,所以
倍,所以![]() ,从而
,从而![]() .
.
联立方程组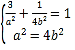 ,解得
,解得![]() ,所以
,所以![]() .
.
(2)设存在这样的常数![]() ,使
,使![]() ,
,![]() 的面积
的面积![]() 为定值.设直线
为定值.设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,点
,点![]() ,则由
,则由![]() 知
知![]() ,
,![]() ,所以
,所以![]() .①
.①
联立方程组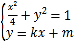 ,消去
,消去![]() 得
得![]() .
.
所以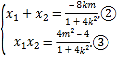 ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]() 的面积
的面积![]() .④
.④
将②③代入①得![]() ,
,
化简得![]() ,⑤
,⑤
将⑤代入④得![]()
![]() ,
,
要使上式为定值,只需![]() ,
,
即需![]() ,从而
,从而![]() ,此时
,此时![]() ,
,![]() ,
,
所以存在这样的常数![]() ,此时
,此时![]() .
.


科目:高中数学 来源: 题型:
【题目】(1)集合![]() ,
,![]() 或
或![]() ,对于任意
,对于任意![]() ,定义
,定义![]() ,对任意
,对任意![]() ,定义
,定义![]() ,记
,记![]() 为集合
为集合![]() 的元素个数,求
的元素个数,求![]() 的值;
的值;
(2)在等差数列![]() 和等比数列
和等比数列![]() 中,
中,![]() ,
,![]() ,是否存在正整数
,是否存在正整数![]() ,使得数列
,使得数列![]() 的所有项都在数列
的所有项都在数列![]() 中,若存在,求出所有的
中,若存在,求出所有的![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)已知当![]() 时,有
时,有![]() ,根据此信息,若对任意
,根据此信息,若对任意![]() ,都有
,都有![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C的顶点在原点,焦点F在y轴上,开口向上,焦点到准线的距离为![]()
(1)求抛物线的标准方程;
(2)已知抛物线C过焦点F的动直线l交抛物线于A、B两点,O为坐标原点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站用“100分制”调查一社区人们的幸福度.现从调查人群中随机抽取10名,以下茎叶图记录了他们的幸福度分数(以十位数字为茎,个位数字为叶);若幸福度不低于95分,则称该人的幸福度为“极幸福”.

(1)从这10人中随机选取3人,记![]() 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)以这10人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记![]() 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求![]() 的数学期望和方差.
的数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应市政府提出的以新旧动能转换为主题的发展战略,某公司花费100万元成本购买了1套新设备用于扩大生产,预计该设备每年收入100万元,第一年该设备的各种消耗成本为8万元,且从第二年开始每年比上一年消耗成本增加8万元.
(1)求该设备使用x年的总利润y(万元)与使用年数x(x∈N*)的函数关系式(总利润=总收入﹣总成本);
(2)这套设备使用多少年,可使年平均利润最大?并求出年平均利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() ,其中点
,其中点![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
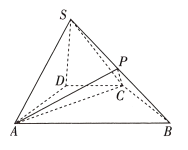
(1)证明:![]() 平面
平面![]() .
.
(2)设点![]() 是线段
是线段![]() (不含端点)上一动点,当三棱锥
(不含端点)上一动点,当三棱锥![]() 的体积为1时,求异面直线
的体积为1时,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
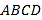
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,其中
,其中![]() ,连接
,连接![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 时,求二面角
时,求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com