练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知M（4，2）是直线l被椭圆x2+4y2=36所截得的线段AB的中点，则直线l的方程为（　　）
    A．2x+y-8=0B．x+2y-8=0C．x-2y-8=0D．2x-y-8=0

    分析 斜率设为 k，则直线l的方程为 y-2=k（x-4），代入椭圆的方程化简，利用韦达定理x1+x2，求出斜率，即可求解直线l的方程．

    解答 解：由题意得，斜率存在，设为 k，则直线l的方程为 y-2=k（x-4），即 kx-y+2-4k=0，
    代入椭圆的方程化简得  （1+4k2）x2+（16k-32k2）x+64k2-64k-20=0，
    ∴x1+x2=$\frac{32{k}^{2}-16k}{1+4{k}^{2}}$=8，解得 k=-$\frac{1}{2}$，
    故直线l的方程为x+2y-8=0，
    故选：B．

    点评 本题考查直线与椭圆的位置关系的应用，韦达定理的应用，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．-1060o的终边落在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

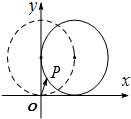    1．如图，在平面直角坐标系xOy中，一单位圆的圆心的初始位置在（0，1），此时圆上一点P的位置在（0，0），圆在x轴上沿正向滚动．当圆滚动到圆心位于（1，1）时，$\overrightarrow{OP}$的坐标为（　　）
    A．（1-sin1，1-cos1）B．（1+sin1，1-cos1）C．（1-sin1，1+cos1）D．（1+sin1，1+cos1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知数列{an}的前项和为an+2=an+1-an，且a1=2，a2=3，Sn为数列{an}的前n项和，则S2017的值为（　　）
    A．0B．2C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．在区间[0，5]上随机地选择一个数t，则方程x2+2tx+3t-2=0有两个负实根的概率为$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知集合M={y|y=2x，x＞0}，N={x|2x-x2≥0}，则M∩N为（　　）
    A．（1，2]B．（1，2）C．[2，+∞）D．[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．中心角为60°的扇形AOB，它的弧长为2π，则三角形AOB的内切圆半径为（　　）
    A．2B．$\sqrt{3}$C．1D．$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．若函数f（x）定义域为R，满足对任意x1，x2∈R，f（x1+x2）≤f（x1）+f（x2）有，则称f（x）为“V形函数”；若函数g（x）定义域为R，g（x）恒大于0，且对任意x1，x2∈R，有lg[g（x1+x2）]≤lg[g（x1）]+lg[g（x2）]，则称g（x）为“对数V形函数”：
    （1）当f（x）=x2时，判断函数f（x）是否为V形函数，并说明理由；
    （2）当g（x）=x2+2时，证明：g（x）是对数V形函数；
    （3）若f（x）是V形函数，且满足对任意x∈R，有f（x）≥2，问f（x）是否为对数V形函数？如果是，请加以证明；如果不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年江西省南昌市高一下学期期末考试数学试卷（解析版） 题型：选择题

    任取一个3位正整数n，则对数log2n是一个正整数的概率为（ ）

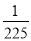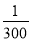    A． B． C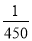． D．以上全不对

    查看答案和解析>>

    同步练习册答案