
���� ��1�������⣬t=0��S=a=7��
��2����Ϊ5����ĩ���δ�ܽ��ǿ������Ϊ3.5�ˣ�����k��ֵ��
��3�����ݺ�������ʽ�ɵú�����ͼ���ɵó����ۣ�
��� �⣺��1�������⣬t=0��S=a=7������7�֣�
��2����Ϊ5����ĩ���δ�ܽ��ǿ������Ϊ3.5�ˣ�
����3.5=7e-5k��
���$k=\frac{ln2}{5}$������2�֣�
��3��M��t�仯�ĺ�����ϵ�IJ�ͼ��ͼ��ʾ���ܽ���̣�����ʱ������ӣ����ܽ⣮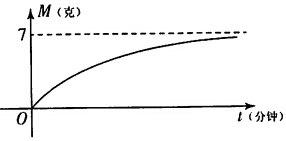 ����5�֣�
����5�֣�
�ʴ�Ϊ��7��
���� ���⿼��������ѧ֪ʶ���ʵ�����⣬����ָ���ͺ����������е��⣮


 �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 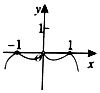 | B�� | 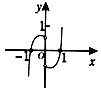 | C�� | 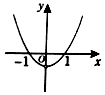 | D�� | 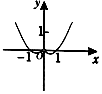 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
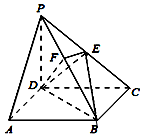 ��ͼ������P-ABCD�ĵ���ABCD�������Σ�����PD�͵���ABCD��PD=DC=2��E��PC���е㣬EF��PB��PB�ڵ�F��
��ͼ������P-ABCD�ĵ���ABCD�������Σ�����PD�͵���ABCD��PD=DC=2��E��PC���е㣬EF��PB��PB�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
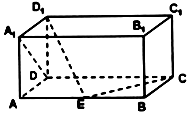 ����ͼ���ڳ�����ABCD-A1B1C1D1�У�AD=AA1=1��AB=2����E����AB���ƶ�����ֱ��D1E��A1D���ɽǵĴ�С��90�㣬��D1E��EC����ֱ��A1D��ƽ��D1DE���ɵĽ�Ϊ30�㣮
����ͼ���ڳ�����ABCD-A1B1C1D1�У�AD=AA1=1��AB=2����E����AB���ƶ�����ֱ��D1E��A1D���ɽǵĴ�С��90�㣬��D1E��EC����ֱ��A1D��ƽ��D1DE���ɵĽ�Ϊ30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5}$ | B�� | 2$\sqrt{5}$ | C�� | 5 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com