若公比为c的等比数列{a
n}的首项a
1=1且满足
an=(n?3,4,…).
(Ⅰ)求c的值;
(Ⅱ)求数列{na
n}的前n项和S
n.
(Ⅰ)由题设,当n≥3时,a
n=c
2a
n-2,a
n-1=ca
n-2,
an==an-2,
由题设条件可得a
n-2≠0,因此
c2=,即2c
2-c-1=0解得c=1或
c=-(Ⅱ)由(Ⅰ),需要分两种情况讨论,
当c=1时,数列{a
n}是一个常数列,即a
n=1(n∈N
*)
这时,数列{na
n}的前n项和
Sn=1+2+3++n=当
c=-时,数列{a
n}是一个公比为
-的等比数列,即
an=(-)n-1(n∈N
*)
这时,数列{na
n}的前n项和
Sn=1+2(-)+3(-)2++n(-)n-1①
1式两边同乘
-2,得
-Sn=-+2(-)2++(n-1)(-)n-1+n(-)n②
①式减去②式,得
(1+)Sn=1+(-)+(-)2++(-)n-1-n(-)n=-n(-)n所以
Sn=[4-(-1)n](n∈N
*)
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
若公比为c的等比数列{a
n}的首项a
1=1且满足
an=(n?3,4,…).
(Ⅰ)求c的值;
(Ⅱ)求数列{na
n}的前n项和S
n.
查看答案和解析>>
科目:高中数学
来源:天津高考真题
题型:解答题
若公比为c的等比数列{a
n}的首项a
1=1且满足a
n=

,
(Ⅰ)求c的值;
(Ⅱ)求数列{na
n}的前n项和S
n。
查看答案和解析>>
科目:高中数学
来源:
题型:
若公比为c的等比数列{a
n}的首项a
1=1且满足a
n=
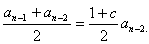
(n=3,4,…).
(1)求c的值;
(2)求数列{nan}的前n项和Sn.
查看答案和解析>>
科目:高中数学
来源:
题型:
若公比为c的等比数列{a
n}的首项a
1=1且满足a
n=
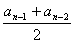
(n=3,4,…).
(1)求c的值;
(2)求数列{nan}的前n项和Sn.
查看答案和解析>>


