
【题目】若平面点集 ![]() 满足:任意点
满足:任意点 ![]() ,存在
,存在 ![]() ,都有
,都有 ![]() ,则称该点集
,则称该点集 ![]() 是“
是“ ![]() 阶聚合”点集。现有四个命题:
阶聚合”点集。现有四个命题:
①若 ![]() ,则存在正数
,则存在正数 ![]() ,使得
,使得 ![]() 是“
是“ ![]() 阶聚合”点集;
阶聚合”点集;
②若 ![]() ,则
,则 ![]() 是“
是“ ![]() 阶聚合”点集;
阶聚合”点集;
③若 ![]() ,则
,则 ![]() 是“2阶聚合”点集;
是“2阶聚合”点集;
④若 ![]() 是“
是“ ![]() 阶聚合”点集,则
阶聚合”点集,则 ![]() 的取值范围是
的取值范围是 ![]() .
.
其中正确命题的序号为( )
A.①④
B.②③
C.①②
D.③④
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,曲线C1的参数方程是 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程是ρ=2sinθ.
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程是ρ=2sinθ.
(Ⅰ) 求曲线C1与C2交点的平面直角坐标;
(Ⅱ) 点A,B分别在曲线C1 , C2上,当|AB|最大时,求△OAB的面积(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”,它是中国古代一个涉及几何体体积问题,意思是两个等高的几何体,如在同高处的截面积恒相等,则体积相等,设A,B为两个等高的几何体,p:A,B的体积相等,q:A,B在同高处的截面积不恒相等,根据祖暅原理可知,q是-p的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差大于零的等差数列{an}的前n项和Sn,且满足a3·a5=112,a1+a7=22.
(1)求等差数列{an}的第七项a7和通项公式an;
(2)若数列{bn}的通项bn=an+an+1,{bn}的前n项和Sn,写出使得Sn小于55时所有可能的bn的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,|an+1-an|=pn,n∈N*,Sn为数列{an}的前n项和.
(1)若{an}是递增数列,且a1,2a2,3a3成等差数列,求p的值;
(2)若p=![]() ,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
(3)在(2)的条件下,令cn=n(an+1-an),求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列 ![]() 中,
中, ![]() ,其前
,其前 ![]() 项和为
项和为 ![]() ,等比数列
,等比数列 ![]() 的各项均为正数,
的各项均为正数, ![]() ,公比为
,公比为 ![]() ,且
,且 ![]() ,
, ![]() .
.
(Ⅰ)求 ![]() 与
与 ![]() .
.
(Ⅱ)设数列 ![]() 满足
满足 ![]() ,求
,求 ![]() 的前
的前 ![]() 项和
项和 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD中,E、F分别是AB、CD上的点,BE=CF=1,BC=2,AB=CD=3,P、Q分别为DE、CF的中点,现沿着EF翻折,使得二面角A﹣EF﹣B大小为 ![]() .
.
(Ⅰ)求证:PQ∥平面BCD;
(Ⅱ)求二面角A﹣DB﹣E的余弦值.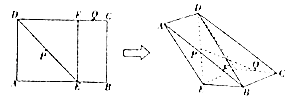
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是数列
是数列 ![]() 的前
的前 ![]() 项和,并且
项和,并且 ![]() ,对任意正整数
,对任意正整数 ![]() ,
, ![]() ,设
,设 ![]() (
( ![]() ).
).
(1)证明:数列 ![]() 是等比数列,并求
是等比数列,并求 ![]() 的通项公式;
的通项公式;
(2)设 ![]() ,求证:数列
,求证:数列 ![]() 不可能为等比数列.
不可能为等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com