【题目】在四棱锥
中，底面
为正方形，
，
为等边三角形，线段
的中点为
，若
，则此四棱锥的外接球的表面积为______.
【答案】
【解析】
设四棱锥
的外接球的球心为
，底面
的中心为
，根据
的相对位置分类讨论，结合锐角三角函数、勾股定理、球和正方形以及矩形的几何性质、球的表面积公式进行求解即可.
设四棱锥的外接球的球心为，其半径为
，底面的中心为.
当位于点
处时，如下图所示：
取
的中点
，连接
，
，因为底面为正方形，
，
为等边三角形，所以
，
，而
，
因为
，所以
，
设正方形的对角线的交点，过
做
平面，
则由题意可知垂足
在上，显然有
，
在直角三角形
中，
，
，所以
过过做
，因此四边形
是矩形，
所以有
，
正方形中，
，
由
可知：
，
在直角三角形
中，得
，
由
解得：
，不符合题意，舍去；
当位于点
处时，如上图所示：
由
可知：
，
在直角三角形中，得
，
由
解得：
，
所以此四棱锥的外接球的表面积为
.
故答案为：
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目：高中数学 来源： 题型：
【题目】已知正项数列
中，
，点
在抛物线
上.数列
中，点
在经过点
，以
为方向向量的直线
上.
（1）求数列，的通项公式；
（2）若
，问是否存在
，使得
成立？若存在，求出
的值；若不存在，说明理由；
（3）对任意的正整数
，不等式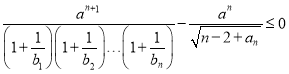
成立，求正数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】新型冠状病毒最近在全国蔓延，具有很强的人与人之间的传染性，该病毒在进入人体后一般有14天的潜伏期，在这14天的潜伏期内患者无任何症状，为病毒传播的最佳时间.假设每位病毒携带者在潜伏期内每天有
位密切接触者，接触病毒携带者后被感染的概率为
，每位密切接触者不用再接触其他病毒携带者.
（1）求一位病毒携带者一天内感染的人数
的均值；
（2）若
，
时，从被感染的第一天算起，试计算某一位病毒携带者在14天潜伏期内，被他平均累计感染的人数（用数字作答）；
（3）3月16日20时18分，由我国军事科学院军事科学研究院陈薇院士领衔的科学团队，研制重组新型冠状病毒疫苗获批进入临床状态，新疫苗的使用，可以极大减少感染新型冠状病毒的人数，为保证安全性和有效性，某科研团队抽取500支新冠疫苗，观测其中某项质量指标值，得到如下频率分布直方图：
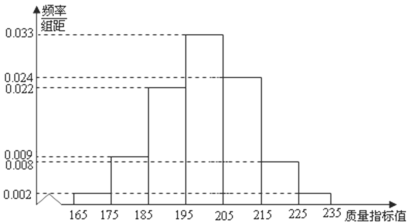
①求这500支该项质量指标值的样本平均值
（同一组的数据用该组区代表间的中点值）
②由直方图可以认为，新冠疫苗的该项质量指标值
服从正态分布
，其中
近似为样本平均数，
近似为样本方差
，经计算可得这500支新冠疫苗该项指标值的样本方差
.现有5名志愿者参与临床试验，观测得出该项指标值分别为：206，178，195，160，229，试问新冠疫苗的该项指标值是否正常，为什么？
参考数据：
，若
，则
，
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知动圆与
轴相切于点
，过点
，
分别作动圆异于轴的两切线，设两切线相交于
，点的轨迹为曲线
.
（1）求曲线的轨迹方程；
（2）过
的直线
与曲线相交于不同两点
，若曲线上存在点
，使得
成立，求实数
的范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】四棱锥P﹣ABCD中，AB∥CD，AB⊥BC，AB＝BC＝1，PA＝CD＝2，PA⊥底面ABCD，E在PB上.
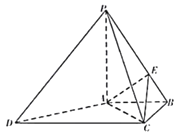
（1）证明：AC⊥PD；
（2）若PE＝2BE，求三棱锥P﹣ACE的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商场为提高服务质量，随机调查了60名男顾客和80名女顾客，每位顾客均对该商场的服务给出满意或不满意的评价，得到下面不完整的列联表：
满意 | 不满意 | 合计 | |
男顾客 | 50 | ||
女顾客 | 50 | ||
合计 |
（1）根据已知条件将列联表补充完整；
（2）能否有
的把握认为男、女顾客对该商场服务的评价有差异？
附：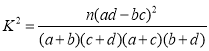
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标平面中，△ABC的两个顶点A、B的坐标分别为A（﹣1，0），B （1，0），平面内两点G、M同时满足下列条件：（1）
；（2）
；（3）
∥
，则△ABC的顶点C的轨迹方程为_____．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】过双曲线C：
1（a＞0，b＞0）右焦点F2作双曲线一条渐近线的垂线，垂足为P，与双曲线交于点A，若
，则双曲线C的渐近线方程为（ ）
A.y＝±
xB.y＝±xC.y＝±2xD.y＝±
x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
