练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （08年福州质检二）（12分）

    已知点A（－2,0），B（2,0），动点P满足：∠APB=2,且|PA||PB|sin2θ=2，

    （Ⅰ）求证：动点P的轨迹Q是双曲线；

    （Ⅱ）过点B的直线与轨迹Q交于两点M，N.试问轴上是否存在定点C，使为常数，若存在，求出点C的坐标；若不存在，说明理由.

     

    解析: （Ⅰ）依题意，由余弦定理得：

    , ……2分

    即

    　　

    .

    ,即.　　…………4分

    （当动点与两定点共线时也符合上述结论）

    动点的轨迹Q是以为焦点,实轴长为的双曲线．其方程为.………6分

    (Ⅱ)假设存在定点,使为常数．

    （1）当直线不与轴垂直时，

    设直线的方程为,代入整理得:

    ．…………7分

    由题意知，．

    设,,则,．…………8分

    于是，   …………9分

    ．…………10分

    要使是与无关的常数，当且仅当，此时．…11分

    （2）当直线与轴垂直时，可得点,，

    当时，．   

    故在轴上存在定点,使为常数.…………12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年福州质检二文）（12分）

    数列的前项和为，满足关系： .

     (Ⅰ)求的通项公式：

     (Ⅱ)设数列的前项和为，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年福州质检二）（12分）

    数列的前项和为，满足关系： .

    (Ⅰ)求的通项公式：

    (Ⅱ)设计算.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年福州质检二）（12分）

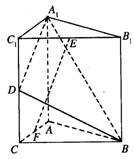
    如图，直三棱柱A1B1C1―ABC中，C1C=CB=CA=2，AC⊥CB. D、E分别为棱C1C、B1C1的中点.

        （Ⅰ）求与平面A1C1CA所成角的大小；

        （Ⅱ）求二面角B―A1D―A的大小；

        （Ⅲ）试在线段AC上确定一点F，使得EF⊥平面A1BD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年福州质检二）（12分）

    已知函数=2acos2x+bsinxcosx，且f(0)=，f()=.

    （Ⅰ）求的解析式；

    （Ⅱ）求的单调递增区间；

    （Ⅲ）函数的图象经过怎样的平移可使其对应的函数成为奇函数？

    查看答案和解析>>

    同步练习册答案