
【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离,
的距离,
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】将![]() 方格表任意一个角上的
方格表任意一个角上的![]() 小方格表挖去,剩下的图形称为“角形”.现在
小方格表挖去,剩下的图形称为“角形”.现在![]() 方格表中放置一些两两不重叠的角形,要求角形的边界与方格表的边界或分格线重合.求正整数
方格表中放置一些两两不重叠的角形,要求角形的边界与方格表的边界或分格线重合.求正整数![]() 的最大值,使得无论以何种方式放置了
的最大值,使得无论以何种方式放置了![]() 个角形之后,总能在方格表中再放入一个完整的角形.
个角形之后,总能在方格表中再放入一个完整的角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,则下列判断中正确的是( )
上运动,则下列判断中正确的是( )

①平面![]() 平面
平面![]() ;
;
②![]() 平面
平面![]() ;
;
③异面直线![]() 与
与![]() 所成角的取值范围是
所成角的取值范围是![]() ;
;
④三棱锥![]() 的体积不变.
的体积不变.
A. ①② B. ①②④ C. ③④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线![]() .以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为
.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为![]() .
.
(1)求C的极坐标方程和曲线M的直角坐标方程;
(2)若M与C只有1个公共点P,求m的值与P的极坐标(![]() ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.

(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)若将频率视为概率,从该企业生产的这种桥梁构件中随机抽取![]() 件,记这
件,记这![]() 件桥梁构件中质量指标值位于区间
件桥梁构件中质量指标值位于区间![]() 内的桥梁构件件数为
内的桥梁构件件数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线![]() .以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为
.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线M的极坐标方程为![]() .
.
(1)求C的极坐标方程和曲线M的直角坐标方程;
(2)若M与C只有1个公共点P,求m的值与P的极坐标(![]() ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学准备组建“文科”兴趣特长社团,由课外活动小组对高一学生文科、理科进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
分成5组,绘制的频率分布直方图如图所示,若将不低于60分的称为“文科方向”学生,低于60分的称为“理科方向”学生.
|
|
(1)根据已知条件完成下面![]() 列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
列联表,并据此判断是否有99%的把握认为是否为“文科方向”与性别有关?
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“文科方向”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
参考公式: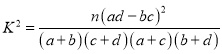 ,其中
,其中![]() .
.
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com