Question

21.已知双曲线的中心在原点,右顶点为A（1,0）,点P、Q在双曲线的右支上,点M（m,0）到直线AP的距离为1.

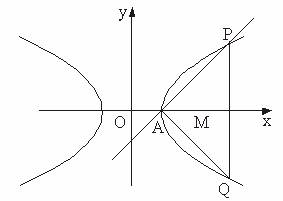
（Ⅰ）若直线AP的斜率为k,且|k|∈［,］,求实数m的取值范围;

（Ⅱ）当m =+1时,△APQ的内心恰好是点M,求此双曲线的方程.

Answer 1

21.本题主要考查直线、双曲线方程和性质等基础知识,考查解析几何的基本思想方法和综合解题能力.

解：（Ⅰ）由条件得直线AP的方程y=k（x－1）,

即kx－y－k=0.

因为点M到直线AP的距离为1,

∴=1,

即|m－1|==.

∵|k|∈［,］,

∴≤|m－1|≤2,

解得+1≤m≤3或－1≤m≤1－.

∴m的取值范围是［－1,1－］∪［1+,3］.

（Ⅱ）可设双曲线方程为x²－=1（b≠0）,

由M（+1,0）,A（1,0）,得|AM|=.

又因为M是△APQ的内心,M到AP的距离为1,所以∠MAP=45°,

直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1.

因此,k_AP=1,k_AQ=－1,（不妨设P在第一象限）

直线PQ方程为x=2+.直线AP的方程y=x－1,

∴解得P的坐标是（2+,1+）.

将P点坐标代入x²－=1得

b²=.

所以所求双曲线方程为x²－y²=1,

即x²－（2－1）y²=1.