练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若存在x∈R，使|2x-a|+2|3-x|≤1成立，则实数a的取值范围是（　　）
    A、[2，4]
    B、（5，7）
    C、[5，7]
    D、（-∞，5]∪[7，+∞）
    考点：绝对值不等式的解法
    专题：不等式的解法及应用
    分析：利用绝对值不等式可得|2x-a|+2|3-x|≥|a-6|，依题意，解不等式|a-6|≤1即可．
    解答：解：∵|2x-a|+2|3-x|=|2x-a|+|6-2x|≥|2x-a+6-2x|=|a-6|，
    ∴|a-6|≤1，
    解得：5≤a≤7．
    ∴实数a的取值范围是[5，7]．
    故选：C．
    点评：本题考查绝对值不等式的解法，求得|2x-a|+2|3-x|≥|a-6|是关键，考查理解与运算能力，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    现有60人，将其编号为01，02，03，…，60，若用系统抽样法从中抽取6人参加某项活动，则抽到的编号可能是（　　）
    A、01，02，04，08，16，32
    B、03，18，23，38，43，58
    C、01，17，27，37，47，57
    D、09，15，21，27，33，39

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    1
    3
    x3-3x，则函数f（x）在区间[-2，2]上取得最大值的点是（　　）
    A、0
    B、-2
    C、2
    D、-
    		3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知tanα=2，那么sin2α的值是（　　）
    A、-
    4
    5
    B、
    4
    5
    C、-
    3
    5
    D、
    3
    5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知cos（x+
    π
    4
    ）=-
    3
    5
    ，则sin2x的值等于（　　）
    A、
    9
    25
    B、-
    9
    25
    C、
    7
    25
    D、-
    7
    25

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个圆的铝盘加热时，随着温度的升高而膨胀，设该圆盘在温度为t℃时，半径为r=r0（1+at）（a为常数），则t℃时，铝盘面积对温度t的变化率是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

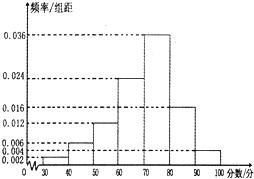    某次月考后，从所有考生中随机抽取50名考生的数学成绩进行统计，并画频率分布直方图，如图所示，则该次考试数学成绩的众数的估计值是（　　）
    A、70
    B、71
    2
    3
    C、75
    D、80

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设x为实数，命题p：?x∈R，x2≥0，则命题p的否定是（　　）
    A、￢p：?x∈R，x2≤0
    B、￢p：?x0∈R，x02≤0
    C、￢p：?x∈R，x2＜0
    D、￢p：?x0∈R，x02＜0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    抛物线C：y2=
    		6
    x，其焦点为F，过点F且与x轴垂直的直线l与C交于A、B两点，点P为不在直线l上的任一点，且|
    PA
    |2+|
    PB
    |2=4，则|2
    PA
    +
    PB
    |2的取值范围是（　　）
    A、（6-3
    		3
    ，6+3
    		3
    ）
    B、[6-3
    		3
    ，6+3
    		3
    ]
    C、（6-3
    		3
    ，6+3
    		3
    ]
    D、[6-3
    		3
    ，6+3
    		3
    ）

    查看答案和解析>>

    同步练习册答案