
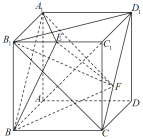
【题目】在正方体![]() 中,点E是棱
中,点E是棱![]() 的中点,点F是线段
的中点,点F是线段![]() 上的一个动点.有以下三个命题:
上的一个动点.有以下三个命题:
①异面直线![]() 与
与![]() 所成的角是定值;
所成的角是定值;
②三棱锥![]() 的体积是定值;
的体积是定值;
③直线![]() 与平面
与平面![]() 所成的角是定值.
所成的角是定值.
其中真命题的个数是( )
A. 3 B. 2 C. 1 D. 0
【答案】B
【解析】
以A点为坐标原点,AB,AD,![]() 所在直线为x轴,y轴,z轴建立空间直角坐标系,
所在直线为x轴,y轴,z轴建立空间直角坐标系,
可得![]() =(1,1,1),
=(1,1,1),![]() =(t-1,1,-t),可得
=(t-1,1,-t),可得![]() =0,可得①正确;
=0,可得①正确;
由三棱锥![]() 的底面
的底面![]() 面积为定值,且
面积为定值,且![]() ∥
∥![]() ,可得②正确;
,可得②正确;
可得![]() =(t,1,-t),平面
=(t,1,-t),平面![]() 的一个法向量为
的一个法向量为![]() =(1,1,1),可得
=(1,1,1),可得![]() 不为定值可得③错误,可得答案.
不为定值可得③错误,可得答案.
解:以A点为坐标原点,AB,AD,![]() 所在直线为x轴,y轴,z轴建立空间直角坐标系,设正方体棱长为1,可得B(1,0,0),C(1,1,O),D(0,1,0),
所在直线为x轴,y轴,z轴建立空间直角坐标系,设正方体棱长为1,可得B(1,0,0),C(1,1,O),D(0,1,0),![]() (0,0,1),
(0,0,1),![]() (1,0,1),
(1,0,1),![]() (1,1,1),
(1,1,1),![]() (0,1,1),设F(t,1,1-t),(0≤t≤1),
(0,1,1),设F(t,1,1-t),(0≤t≤1),
可得![]() =(1,1,1),
=(1,1,1),![]() =(t-1,1,-t),可得
=(t-1,1,-t),可得![]() =0,故异面直线
=0,故异面直线![]() 与
与![]() 所的角是定值,故①正确;
所的角是定值,故①正确;
三棱锥![]() 的底面
的底面![]() 面积为定值,且
面积为定值,且![]() ∥
∥![]() ,点F是线段
,点F是线段![]() 上的一个动点,可得F点到底面
上的一个动点,可得F点到底面![]() 的距离为定值,故三棱锥
的距离为定值,故三棱锥![]() 的体积是定值,故②正确;
的体积是定值,故②正确;
可得![]() =(t,1,-t),
=(t,1,-t),![]() =(0,1,-1),
=(0,1,-1),![]() =(-1,1,0),可得平面
=(-1,1,0),可得平面![]() 的一个法向量为
的一个法向量为![]() =(1,1,1),可得
=(1,1,1),可得![]() 不为定值,故③错误;
不为定值,故③错误;
故选B.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C的参数方程为![]() 为参数
为参数![]() ,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
(1)求曲线C的极坐标方程;
(2)设直线l的极坐标方程为![]() ,若直线l与曲线C交于M,N两点,且
,若直线l与曲线C交于M,N两点,且![]() ,求直线l的直角坐标方程.
,求直线l的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程.
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式用最小二乘法求线性回归方程系数公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两名工人在同样条件下每天各生产100件产品,且每生产1件正品可获利20元,生产1件次品损失30元,甲、乙两名工人100天中出现次品件数的情况如表所示.
甲每天生产的次品数/件 | 0 | 1 | 2 | 3 | 4 |
对应的天数/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生产的次品数/件 | 0 | 1 | 2 | 3 |
对应的天数/天 | 30 | 25 | 25 | 20 |
(1)将甲每天生产的次品数记为![]() (单位:件),日利润记为
(单位:件),日利润记为![]() (单位:元),写出
(单位:元),写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)按这100天统计的数据,分别求甲、乙两名工人的平均日利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 汉字听写大会
汉字听写大会![]() 不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试
不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试![]() 现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组
现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,
,![]() ,第6组
,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

![]() 若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
![]() 试估计该市市民正确书写汉字的个数的平均数与中位数;
试估计该市市民正确书写汉字的个数的平均数与中位数;
![]() 已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系内的动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离比为
的距离比为![]() .
.
(1)求动点P所在曲线E的方程;
(2)设点Q为曲线E与![]() 轴正半轴的交点,过坐标原点O作直线
轴正半轴的交点,过坐标原点O作直线![]() ,与曲线E相交于异于点
,与曲线E相交于异于点![]() 的不同两点
的不同两点![]() ,点C满足
,点C满足![]() ,直线
,直线![]() 和
和![]() 分别与以C为圆心,
分别与以C为圆心,![]() 为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比
为半径的圆相交于点A和点B,求△QAC与△QBC的面积之比![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com