
分析:双曲线与椭圆有共同的焦点,可对双曲线定位及求得c,由c2=a2+b2,因而再有一个条件即可求得方程,可求出交点,联立方程组求a2,b2,或利用双曲线的定义求a,
解法一:
椭圆![]() 的两个焦点为F1(0,-3)、F2(0,3),双曲线与椭圆的一个交点为A(
的两个焦点为F1(0,-3)、F2(0,3),双曲线与椭圆的一个交点为A(![]() ,4).
,4).
设双曲线的方程为![]() (a>0,b>0),
(a>0,b>0),
由方程组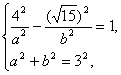
得
∴双曲线的方程为![]()
解法二:
F1(0,-3)、F2(0,3)、A(![]() ,4)的得出同解法一.
,4)的得出同解法一.
设双曲线的方程为![]() (a>0,b>0),则
(a>0,b>0),则
2a=||AF1|-|AF2||
![]()
∴a=2,b2=c2-a2=32-22=5.
∴双曲线的方程为![]()
解法三:
设双曲线的方程为![]() ①
①
将A(![]() ,4)代入①,得λ1=32,λ2=0(舍去).
,4)代入①,得λ1=32,λ2=0(舍去).
∴双曲线的方程为![]()
绿色通道:
本题给出了三种解法,前两种为常规方法,第三种方法是抓住与椭圆有公共的焦点这个条件来设双曲线方程.


科目:高中数学 来源:2012-2013学年黑龙江省大庆35中高二(上)期中数学试卷(解析版) 题型:解答题
 有共同的焦点,且与椭圆相交,在第一象限的交点A的纵坐标为4,求此双曲线的方程.
有共同的焦点,且与椭圆相交,在第一象限的交点A的纵坐标为4,求此双曲线的方程.查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省泉州市南安市诗山中学高二(上)第三次月考数学试卷(解析版) 题型:解答题
 有共同的焦点,且与椭圆相交,在第一象限的交点A的纵坐标为4,求此双曲线的方程.
有共同的焦点,且与椭圆相交,在第一象限的交点A的纵坐标为4,求此双曲线的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com