
����Ŀ����һ�γ��������в��������6�����ݣ��õ�һ������![]() ����
����![]() �Ļع鷽��ģ�ͣ����Ӧ����ֵ���±���
�Ļع鷽��ģ�ͣ����Ӧ����ֵ���±���
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)�������ϵ��![]() ����˵��
����˵��![]() ��
��![]() ֮�����������ع�ϵ(��
֮�����������ع�ϵ(��![]() ʱ��˵��
ʱ��˵��![]() ��
��![]() ֮�����������ع�ϵ)��
֮�����������ع�ϵ)��
(2)����(1)���жϽ��������![]() ����
����![]() �Ļع鷽�̲�Ԥ�
�Ļع鷽�̲�Ԥ�![]() ʱ����Ӧ��
ʱ����Ӧ��![]() ֵΪ����(
ֵΪ����(![]() ��ȷ��
��ȷ��![]() ).
).
���ο���ʽ���ع鷽��![]() ��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
 ��
��![]() �����ϵ��
�����ϵ��![]() ��ʽΪ��
��ʽΪ��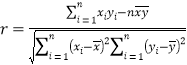 .
.
�ο����ݣ�
![]() ��
��![]() ��
��![]() ��
��![]() .
.
 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ϵ�ļ�����ֱ������ϵ��ԭ�㴦��������x��Ǹ������غϣ�ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��ԲC�IJ�������Ϊ
��ԲC�IJ�������Ϊ![]() ��
��
��1����ֱ��![]() ��ԲC���صõ��ҳ���
��ԲC���صõ��ҳ���
��2����֪��![]() ������
������![]() ��ֱ��
��ֱ��![]() ��Բ���ཻ��
��Բ���ཻ��![]() ��ͬ�����㣬��
��ͬ�����㣬��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�����Уѧ��ÿ��ʹ���ֻ�������ʱ�䣬����ռ�������λѧ��ÿ��ʹ���ֻ�������ʱ����������ݣ���λ��Сʱ�������������ݷ���Ϊ![]() ������������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����֪
������������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����֪![]() �ڵ�ѧ����5�ˣ�
�ڵ�ѧ����5�ˣ�

��1������������![]() �������Ƹ�Уѧ��ÿ��ƽ��ʹ���ֻ�������ʱ�䣻
�������Ƹ�Уѧ��ÿ��ƽ��ʹ���ֻ�������ʱ�䣻
��2����ʹ���ֻ�������ʱ����![]() �ڶ���Ϊ����ʱ�俴�ֻ�����ʹ���ֻ�������ʱ����
�ڶ���Ϊ����ʱ�俴�ֻ�����ʹ���ֻ�������ʱ����![]() �ڶ���Ϊ������ʱ�俴�ֻ�������֪����������
�ڶ���Ϊ������ʱ�俴�ֻ�������֪����������![]() λѧ�������ӣ����С�����ʱ�俴�ֻ�������
λѧ�������ӣ����С�����ʱ�俴�ֻ�������![]() λѧ�����뽫�����
λѧ�����뽫�����![]() �������������������ж��ܷ��ڷ�����ĸ��ʲ�����
�������������������ж��ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ��Уѧ����ʱ�俴�ֻ�������йأ�
��ǰ������Ϊ��Уѧ����ʱ�俴�ֻ�������йأ�
���� | ������ | �ϼ� | |
��ʱ�俴�ֻ� | |||
����ʱ�俴�ֻ� | 15 | ||
�ϼ� | 25 |
�ο���ʽ�����ݣ�![]() ��
��
|
|
|
|
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1��������![]() ��ͼ����
��ͼ����![]() �������߷���Ϊ
�������߷���Ϊ![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
��2����![]() ��
��![]() ��ʹ
��ʹ![]() ��������
��������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���������
���������![]() ����
����![]() ����
����![]() ʱ����
ʱ����![]() ��
��![]()
��1���ж�![]() ����ż�ԣ�
����ż�ԣ�
��2����![]() ��
��![]() �ϵ����ֵ��
�ϵ����ֵ��
��3�������![]() �IJ���ʽ
�IJ���ʽ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lnx��![]() ��
��
��1����a��0�����ж�f��x���ڶ������ڵĵ����ԣ�
��2����f��x����[1��e]�ϵ���СֵΪ![]() ����ʵ��a��ֵ��
����ʵ��a��ֵ��
��3����f��x����x2�ڣ�1��+�ޣ��Ϻ��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ϵ�����һ�㵽������
�ϵ�����һ�㵽������![]() ��
��![]() ����֮��Ϊ
����֮��Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() ��
��![]() ���㣬
���㣬![]() Ϊ����ԭ�㣮
Ϊ����ԭ�㣮
��1��������![]() �ķ��̣�
�ķ��̣�
��2����![]() ������
������![]() �Ҳ�ƽ���������ᣬ���߶�
�Ҳ�ƽ���������ᣬ���߶�![]() ���е�Ϊ
���е�Ϊ![]() ����֤��ֱ��
����֤��ֱ��![]() ��б����
��б����![]() ��б�ʵij˻�Ϊ��ֵ��
��б�ʵij˻�Ϊ��ֵ��
��3����ֱ��![]() ����
����![]() ����
����![]() ��������ֵ���Լ�ȡ���ֵʱֱ��
��������ֵ���Լ�ȡ���ֵʱֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() =1��a��b��0����e=
=1��a��b��0����e= ![]() ������F����Բ���ҽ��㣬����Ϊ2��ֱ��l����ԲC���ڵ�A��B����A��B���е������Ϊ
������F����Բ���ҽ��㣬����Ϊ2��ֱ��l����ԲC���ڵ�A��B����A��B���е������Ϊ ![]() ����
���� ![]() =��
=�� ![]() �����Цˣ�1����
�����Цˣ�1����
��1������ԲC�ı����̣�
��2����ʵ���˵�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ����
����![]() ��
��![]() ��
��![]() ���㣮
���㣮
(1)��Բ![]() �ı����̣�
�ı����̣�
(2)������N ![]() ��ֱ��
��ֱ��![]() ��Բ
��Բ![]() �صõ���AB�ij�Ϊ
�صõ���AB�ij�Ϊ![]() ����ֱ��
����ֱ��![]() ����б�ǣ�
����б�ǣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com