
【题目】某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等制划分标准为:85分及以上,记为![]() 等;分数在
等;分数在![]() 内,记为
内,记为![]() 等;分数在
等;分数在![]() 内,记为
内,记为![]() 等;60分以下,记为
等;60分以下,记为![]() 等.同时认定
等.同时认定![]() 为合格,
为合格, ![]() 为不合格.已知甲,乙两所学校学生的原始成绩均分布在
为不合格.已知甲,乙两所学校学生的原始成绩均分布在![]() 内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计,按照
内,为了比较两校学生的成绩,分别抽取50名学生的原始成绩作为样本进行统计,按照![]() 的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为
的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为![]() 的所有数据茎叶图如图2所示.
的所有数据茎叶图如图2所示.
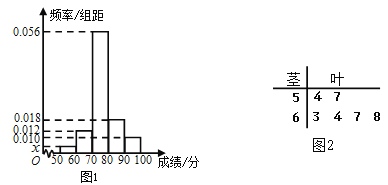
(Ⅰ)求图1中![]() 的值,并根据样本数据比较甲乙两校的合格率;
的值,并根据样本数据比较甲乙两校的合格率;
(Ⅱ)在选取的样本中,从甲,乙两校![]() 等级的学生中随机抽取3名学生进行调研,用
等级的学生中随机抽取3名学生进行调研,用![]() 表示所抽取的3名学生中甲校的学生人数,求随机变量
表示所抽取的3名学生中甲校的学生人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;甲、乙两校的合格率均为96%;(2)详见解析.
;甲、乙两校的合格率均为96%;(2)详见解析.
【解析】试题分析:(1)频率分布直方图中,小矩形的和为频率和,和为1,这样可得到![]() 的值;合格率为大于等于60分的频率和;(2)
的值;合格率为大于等于60分的频率和;(2)![]() 为
为![]() 级,甲校C级的频率为
级,甲校C级的频率为![]() ,人数为
,人数为![]() ,而乙校C级的人数为4人,随机抽取3人中,甲校学生人数
,而乙校C级的人数为4人,随机抽取3人中,甲校学生人数![]() 的可能取值为0,1,2,3,所对应的概率
的可能取值为0,1,2,3,所对应的概率![]() ,列分布列并求数学期望.
,列分布列并求数学期望.
试题解析:(1)由题意,可知![]() ,
,
∴![]() ................2分
................2分
∴甲学校的合格率为![]() ........................3分
........................3分
而乙学校的合格率为![]() .................4分
.................4分
∴甲、乙两校的合格率均为96%................5分
(2)样本中甲校![]() 等级的学生人数为
等级的学生人数为![]() ....................6分
....................6分
而乙校![]() 等级的学生人数为4.
等级的学生人数为4.
∴随机抽取3人中,甲校学生人数![]() 的可能取值为0,1,2,3...........7分
的可能取值为0,1,2,3...........7分
∴![]() ,
,
∴![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
...................................11分
数学期望![]() .................12分
.................12分


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:
【题目】某厂拟生产甲、乙两种适销产品,每件销售收入分别为3万元、2万元,甲、乙产品都需要在![]() 两种设备上加工,在每台
两种设备上加工,在每台![]() 上加工1件甲所需工时分别是1
上加工1件甲所需工时分别是1![]() 、2
、2![]() ,加工1件乙所需工时分别为2
,加工1件乙所需工时分别为2![]() 、1
、1![]() ,
, ![]() 两种设备每月有效使用台时数分别为400
两种设备每月有效使用台时数分别为400![]() 和500
和500![]() ,如何安排生产可使收入最大?
,如何安排生产可使收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(II)设函数![]() 存在两个极值点,并记作
存在两个极值点,并记作![]() ,若
,若![]() ,求正数
,求正数![]() 的取值范围;
的取值范围;
(III)求证:当![]() =1时,
=1时, ![]() (其中e为自然对数的底数)
(其中e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1.
(I)求证:直线MN//平面CAB1;
(II)求证:直线BA1⊥平面CAB1.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在x=1处的切线与直线
在x=1处的切线与直线![]() 平行。
平行。
(Ⅰ)求a的值并讨论函数y=f(x)在![]() 上的单调性。
上的单调性。
(Ⅱ)若函数![]() (
(![]() 为常数)有两个零点
为常数)有两个零点![]() ,
,
(1)求m的取值范围;
(2)求证: ![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形![]() 的底角
的底角 ![]() 等于
等于![]() ,直角梯形
,直角梯形 ![]() 所在的平面垂直于平面
所在的平面垂直于平面![]() ,
, ![]() ,且
,且![]() .
.
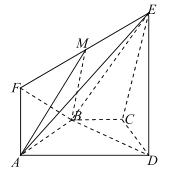
(1)证明:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,试确定点
上,试确定点![]() 的位置,使平面
的位置,使平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com