[题目]等差数列{an}的前n项和为Sn . 若a7＞0.a8＜0.则下列结论正确的是( )A.S7＜S8B.S15＜S16C.S13＞0D.S15＞0 题目和参考答案——青夏教育精英家教网—

【题目】等差数列{an}的前n项和为Sn ，若a7＞0，a8＜0，则下列结论正确的是( )
A.S7＜S8
B.S15＜S16
C.S13＞0
D.S15＞0

【答案】C
【解析】解答：根据数列的增减性，由已知可知该等差数列{an}是递减的，且S7最大即Sn≤S7对一切n∈N*恒成立．可见选项A错误；易知a16＜a15＜0，S16＝S15＋a16＜S15 ，选项B错误；S15＝ (a1＋a15)＝15a8＜0，选项D错误；S13＝ (a1＋a13)＝13a7＞0.
分析：因为公差非零的等差数列具有单调性(递增数列或递减数列)，根据数列的增减性，即可.
【考点精析】认真审题，首先需要了解等差数列的前n项和公式(前n项和公式：)．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数

（1）若函数的图像在公共点P处有相同的切线，求实数m的值和P的坐标；

（2）若函数的图像有两个不同的交点M、N，求实数m的取值范围；

（3）在（2）的条件下，过线段MN的中点作x轴的垂线分别与的图像和的图象交于S、T点，以S点为切点作以T为切点作的切线，是否存在实数m，使得？如果存在，求出m的值；如果不存在，请说明理由。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】写出下列各组命题构成的“p或q”、“p且q”以及“非p”形式的命题，并判断它们的真假．
（1）是有理数，q：是整数；
（2）不等式x2－2x－3>0的解集是(－∞，－1)，q：不等式x2－2x－3>0的解集是(3，＋∞)．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列{an}满足an = nkn(n∈N* ， 0 < k < 1)，下面说法正确的是( )
①当时，数列{an}为递减数列；
②当时，数列{an}不一定有最大项；
③当时，数列{an}为递减数列；
④当为正整数时，数列{an}必有两项相等的最大项.
A.①②
B.②④
C.③④
D.②③

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在圆上任取一点，过点向轴作垂线段，垂足为，当点在圆上运动时，线段的中点的轨迹为.

(1)求曲线的方程；

(2)过点(0，－2)作直线与交于两点，(O为原点)，求三角形面积的最大值，并求此时的直线的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】叙利亚内战接近尾声，中国红十字会相应国际号召，支持叙利亚人民战后重建，为解决现阶段叙利亚人民急需的医疗保障，现拟从北京某知名医院的专职教授的医生6人（其中男医生3人，女医生3人），护士8人（其中男护士2人，女护士6人）中选派医生、护士各三人组成卫生医疗对，要求男医生至少两人，男护士至少一人，则这样的选派方案共有__________种．（请用数字作答）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知为等差数列，公差（），且（）
（1）求证：当取不同自然数时，此方程有公共根；
（2）若方程不同的根依次为，，， …，， …，求证：数列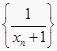为等差数列。