
【题目】将函数y=sin2x-cos2x的图象向左平移m(m>0)个单位以后得到的图象与函数y=ksinxcosx(k>0)的图象关于(![]() ,0)对称,则k+m的最小正值是
,0)对称,则k+m的最小正值是
A. 2+![]() B. 2+
B. 2+![]() C. 2+
C. 2+![]() D. 2+
D. 2+![]()
【答案】C
【解析】
由题意可得y=﹣cos(2x﹣2m)的图象和y=![]() sin2x(k>0)的图象关于点
sin2x(k>0)的图象关于点![]() 对称,设点
对称,设点
P(x0,y0)为y=﹣cos(2x﹣2m)上任意一点,则该点关于![]() 对称点为
对称点为![]() 在
在
y=![]() sin2x(k>0)的图象上,故有
sin2x(k>0)的图象上,故有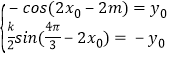 ,求得k=2,且cos(2x0﹣
,求得k=2,且cos(2x0﹣![]() )=cos
)=cos
(2x0﹣2m),由此求得k+m的最小正值.
将函数y=sin2x﹣cos2x=﹣cos2x的函数图象向右平移m个单位以后得到y=﹣cos2(x﹣m)=
﹣cos(2x﹣2m)的图象,
根据所得图象与y=ksinxcosx=![]() sin2x(k>0)的图象关于
sin2x(k>0)的图象关于![]() 对称,
对称,
设点P(x0,y0)为y=﹣cos(2x﹣2m)上任意一点,
则该点关于![]() 对称点为
对称点为![]() 在y=
在y=![]() sin2x(k>0)的图象上,故有
sin2x(k>0)的图象上,故有
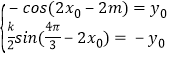 ,
,
所以k=2,sin(2x0﹣![]() )=cos(2x0﹣2m),即cos(2x0﹣
)=cos(2x0﹣2m),即cos(2x0﹣![]() )=cos(2x0﹣2m),
)=cos(2x0﹣2m),
∴﹣2m=﹣![]() +2kπ,k∈Z,即 2m=
+2kπ,k∈Z,即 2m=![]() ﹣2kπ,k∈Z,故m的最小正值为
﹣2kπ,k∈Z,故m的最小正值为![]() ,
,
则k+m的最小正值为2+![]() .故答案为:C
.故答案为:C


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】即将开工的南昌与周边城镇的轻轨火车路线将大大缓解交通的压力,加速城镇之间的流通.根据测算,如果一列火车每次拖4节车厢,每天能来回16次;如果一列火车每次拖7节车厢,每天能来回10次,每天来回次数![]() 是每次拖挂车厢个数
是每次拖挂车厢个数![]() 的一次函数.
的一次函数.
(1)写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)每节车厢一次能载客110人,试问每次应拖挂多少节车厢才能使每天营运人数![]() 最多?并求出每天最多的营运人数(注:营运人数指火车运送的人数)
最多?并求出每天最多的营运人数(注:营运人数指火车运送的人数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() .记
.记![]() .给出下列关于函数
.给出下列关于函数![]() 的说法:①当
的说法:①当![]() 时,
时,![]() ;②函数
;②函数![]() 为奇函数;③函数
为奇函数;③函数![]() 在
在![]() 上为增函数;④函数
上为增函数;④函数![]() 的最小值为
的最小值为![]() ,无最大值.其中正确的是______.
,无最大值.其中正确的是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “f(0)![]() ”是“函数f(x)是奇函数”的充要条件
”是“函数f(x)是奇函数”的充要条件
B. 若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
C. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,四边形ABCD为菱形,△PAD为正三角形,且E为AD的中点,BE⊥平面PAD.

(Ⅰ)求证:平面PBC⊥平面PEB;
(Ⅱ)求平面PEB与平面PDC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且当点
两点,且当点![]() 是椭圆
是椭圆![]() 的上顶点时,
的上顶点时,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)延长线段![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,若
,若![]() ,求此时
,求此时![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知a,b,N都是正数,a≠1,b≠1,证明对数换底公式:logaN=![]() ;
;
(2)写出对数换底公式的一个性质(不用证明),并举例应用这个性质.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com