
 如图所示,A,B是椭圆的两个顶点,C是AB的中点,F为椭圆的右焦点,OC的延长线交椭圆于点M,且|OF|=
如图所示,A,B是椭圆的两个顶点,C是AB的中点,F为椭圆的右焦点,OC的延长线交椭圆于点M,且|OF|=| 2 |
| x2 |
| 4 |
| y2 |
| 2 |
| x2 |
| 4 |
| y2 |
| 2 |
| 2 |
| 2 |
| x2 |
| b2+2 |
| y2 |
| b2 |
| 2 |
| b2+2 |
| y2 |
| b2 |
| b2 | ||
|
| 2 |
| b2 | ||
|
| b2+2 |
| ||
| 2 |
| b |
| 2 |
| ||||
|
| ||||
|
| 2 |
| x2 |
| 4 |
| y2 |
| 2 |
| x2 |
| 4 |
| y2 |
| 2 |


科目:高中数学 来源: 题型:
(08年湖北卷理)如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
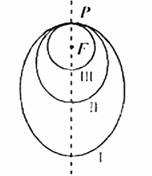
①a1+c1=a2+c2;②a1-c1=a2-c2;③c1a2>a1c1;④![]() <
<![]() .
.
其中正确式子的序号是
A.①③ B.②③ C.①④ D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①a1+c1=a2+c2;②a1-c1=a2-c2;③c1a2>a1c1;④![]() <
<![]() 。
。
其中正确式子的序号是

A.①③ B.②③ C.①④ D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①a1+c1=a2+c2;②a1-c1=a2-c2;③c1a2>a1c1;④![]() <
<![]() 。
。
其中正确式子的序号是

A.①③ B.②③ C.①④ D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
简化的北京奥运会主体育场 “鸟巢”的钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,外层椭圆顶点向内层椭圆引切线![]() .设内层椭圆方程为
.设内层椭圆方程为![]() ,则外层椭 圆方程可设为
,则外层椭 圆方程可设为![]() .若
.若![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,则椭圆的离心率为 ( )
,则椭圆的离心率为 ( )

(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(湖北卷) 题型:选择题
如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①a1+c1=a2+c2;②a1-c1=a2-c2;③c1a2>a1c1;④ <
< 。
。
其中正确式子的序号是

A.①③ B.②③ C.①④ D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com